Abstract: Quantitative methods are used in business for many years from the middle of the 20th century. With the development of electronic computers, it became possible to model complex enterprise management systems. Knowledge and use of quantitative methods of developing and making managerial decisions is one of the important competences of a modern manager. In this article, the application of mathematical models for making managerial decisions under conditions of certainty, risk and uncertainty is considered.
Keywords: Management, modeling, management decisions, quantitative methods.
Акцент на использование количественных методов разработки и принятия решений сложных проблем в управлении характерен для научного менеджмента, отличительными особенностями которого являются следующие:
- системный взгляд на проблему, принятие во внимание всех имеющихся точек зрения, всех существенных взаимосвязанных переменных, содержащихся в решаемой задаче;
- командный подход к решению проблем на основе совместной разработки возможных альтернатив и их обсуждения;
- акцент на использовании формальных математических моделей и статистических и количественных методов анализа.
Модель является абстракцией или упрощенным представлением существующей реальности, разработанной, чтобы включать только существенные черты, которые определяют поведение реальной системы.
Большинство моделей научного менеджмента являются математическими. Они могут быть составлены из общего уравнения, представляющего финансовые операции компании:
чистая прибыль= выручка — затраты — налоги.
В научном менеджменте используется пятиступенчатый процесс моделирования, который начинается в реальном мире и развивается в модельном мире, чтобы решить поставленную проблему, а затем возвращается в реальный мир для реализации принятого решения. Концептуальный подход к моделированию в менеджменте предполагает последовательное прохождение по следующим этапам:
- формулировка задачи (определение целей, переменных и ограничений);
- построение математической модели (на основе упрощенного реалистичного представления о рассматриваемой системе);
- проверка способности модели предсказывать явления из прошлого, и ее пересмотр в случае необходимости;
- анализ последствий различных вариантов принятых решения на базе составленной модели и выбор оптимального решения;
- реализация выбранного оптимального решения на практике. В случае несоответствия последствий, выявленных в процессе моделирования, реальным последствиям – пересмотр модели.
Научный метод или научный процесс имеет фундаментальное значение для менеджмента. Можно выделить три категории принятия управленческих решений:
- в условиях определенности;
- в условиях риска;
- в условиях неопределенности.
В общем виде процесс разработки и принятия управленческих решений можно представить в виде таблицы выигрышей или матрицы решений (табл. 1).
Таблица 1.
Матрица решений
| Альтернативы | Последствия/Вероятность | |||||
| N1 | N2 | … | Nj | … | Nn | |
| p1 | p2 | … | pj | … | pn | |
| A1 | O11 | O12 | … | O1j | … | O1n |
| A2 | O21 | O12 | … | O2j | … | O2n |
| … | … | … | … | … | ||
| Ai | Oi1 | Oi2 | … | Oij | … | Oin |
| … | … | … | … | … | ||
| Am | Om1 | Om2 | … | Omj | … | Omn |
Как видно из табл. 1, решение принимается среди некоторого числа (m) альтернатив, которые записываются как A1 A2, …, Am. Будущая ситуация, положение дел или последствия принятия различных решений обозначены как N, их количество составляет n последствий. Эти последствия не могут быть в равной степени вероятны, и каждое из них (Nj) имеет некоторую (известную или неизвестную) вероятность Pj, сумма которых составляет 1.
Исход (получаемая выгода или выигрыш) будет зависеть как от выбранной альтернативы, так и от последствий. Например, если выбрана альтернатива Ai и будет реализовано последствие Nj с вероятностью Pi, то выигрыш составит Qij. Полная матрица решений будет содержать m альтернатив n последствий.
Рассмотрим применение представленной модели для принятие различных категорий управленческих решений.
Категория 1. Принятие управленческих решений в условиях определенности. Принятие решений в условиях определенности предполагает, что мы уверены в будущих последствиях принятия различных решений (или мы предполагаем, что это так). В нашей модели это означает, что вероятность р1 будущего Ni составляет 1, а все остальные последствия имеют нулевую вероятность. Решение очевидно – выбрать альтернативу Ai, которая дает нам наиболее благоприятный исход Oij.
Распространенным методом для принятия решений в условиях определенности является линейное программирование. В этом способе желаемый исход (например, определенная сумма прибыли) может быть выражен в виде математической функции (целевой функции) с несколькими переменными.
Решение представляет собой множество значений независимых переменных (переменных решения), которое служит для максимизации выгоды (или из-за многочисленных проблем, для сведения к минимуму расходов), при соблюдении определенных ограничений.
Категория 2. Принятие управленческих решений в условиях риска. В процессе принятия решений в условиях риска предполагается, что существует ряд возможных будущих состояний (последствий) Nj в соответствии с матрицей риска. Каждое последствие имеет свою определенную вероятность pj и может быть только одно последствие, которое приводит к лучшему результату для всех альтернатив Ai. Примеры будущих состояний и их вероятностей могут быть записаны следующим образом:
- Альтернативная погода (N1 = дождь; N2 = хорошая погода) будет влиять на рентабельность альтернативных графиков строительства. Здесь вероятность p1 дождя и р2 хорошей погоды можно оценить на основе исторических данных;
- Альтернативные варианты экономической ситуации в стране определяют относительную прибыльность инвестиционной стратегии предприятия. Здесь предполагаемые вероятности различных вариантов экономической ситуации могут основываться на суждениях экспертов-экономистов.
Учитывая последствия принятия решений и их вероятность, принятие решения в условиях риска является альтернативой Ai, которая обеспечивает высокий ожидаемый результат Ei, которая раcсчитывается как сумма произведений каждого из результатов Oij на вероятность pj каждого из возможных последствий Nj и может быть записана следующим образом:
Ei=∑nj=1(pj* Oij) (1)
Для принятия решений в условиях риска можно также использовать другую технику – дерево решений. Для начала необходимо составить так называемый узел решений (обычно в виде квадрата или прямоугольника), из которого можно получить количество альтернативных вариантов решений. Каждая альтернатива заканчивается случайным узлом, как правило, изображаемым в виде круга.
Из каждого узла можно излучать несколько возможных вариантов будущего, их вероятность и конечный результат. Ожидаемый результат для каждой альтернативы является суммой произведений результатов и связанных с ними вероятностей.
Другим распространенным смыслом принятия решений в условиях риска является изменчивость результатов, которая определяется с помощью нахождения дисперсии – квадратного корня стандартного отклонения.
Рассмотрим два инвестиционных проекта: X и Y, характеризующихся распределением вероятностей ожидаемых денежных потоков в каждом из следующих нескольких лет, как показано в табл. 2.
Таблица 2.
Данные риска и дисперсии
| Проект X | Проект Y | ||
| Вероятность | Денежный поток, тыс. руб. | Вероятность | Денежный поток, тыс. руб. |
| 0,10 | 3000 | 0,10 | 2000 |
| 0,20 | 3500 | 0,25 | 3000 |
| 0,40 | 4000 | 0,30 | 4000 |
| 0,20 | 4500 | 0,25 | 5000 |
| 0,10 | 5000 | 0,10 | 6000 |
Ожидаемые денежные потоки рассчитываются таким же образом, как и ожидаемый результат:
E (X) = 0,10*(3000) + 0,20*(3500) + 0,40*(4000) + 0,20*(4500) + 0,10*(5000)= 4000 тыс. руб.
E (Y) = 0,10*(2000) + 0,25*(3000) + 0,30*(4000) + 0,25*(5000) + 0,10*(6000)= 4000 тыс. руб.
Несмотря на то, что оба проекта имеют одинаковые средние (ожидаемые) денежные потоки, ожидаемые результаты дисперсий (квадратов отклонений от среднего значения) отличаются:
Vx=0,10*(3000-4000)2+0,20*(3500-4000)2+…+0,10*(5000-4000)2= =300000 тыс. руб.
Vy=0,10*(2000-40000)2+0,25*(3000-4000)2+…+0,10*(6000-4000)2= =1300000 тыс. руб.
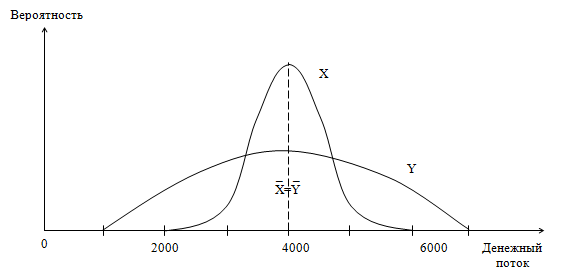
Стандартные отклонения – это квадратные корни этих значений (рис. 1).
Рисунок 1. Проекты с одинаковыми ожидаемыми результатами, но разной вариацией
Так проект Y имеет большую изменчивость (дисперсию), то он характеризуется большим риском, чем проект Х, который является предпочтительным в данной ситуации, так как предлагает тот же ожидаемый результат с меньшим риском.
Категория 3. Принятие управленческих решений в условиях неопределенности.
В некоторых ситуациях менеджер не может оценить вероятность возникновения различных последствий. Неопределенность возникает, когда существует несколько (то есть, больше чем один) будущих последствий Nj, но вероятность pj каждого них неизвестна. В таких ситуациях менеджер может выбрать один из нескольких возможных подходов к принятию решения. Можно выделить следующие основные подходы к принятию управленческих решений в условиях неопределенности:
- оптимистический подход к принятию управленческих решений – выбор того варианта, который предлагает самое лучшее из возможных последствий (решение «maximax»);
- пессимистический подход к принятию управленческих решений – выбор альтернативы, последствия которой наименее плохие (решение «maximin»);
- подход Гурвица к принятию управленческих решений – выбор среднего решения между оптимистическим и пессимистическим;
- подход недостаточного основания для принятия управленческих решений – предполагается, что все последствия равновероятны (pj=1/n) и выбирается альтернатива, предполагающая максимальный ожидаемый результат;
- подход утраченных возможностей – выбор решения, последствия которого характеризуются наименьшей разницей между лучшими и худшими результатами (решение «разница minimax»). В результате принятое решение пропорционально разнице между тем, что мы на самом деле хотим получить, и лучшим из возможных последствий.
В рамках оптимистического подхода менеджер будет стремиться к «maximax», выбрав лучший. В рамках пессимистического подхода менеджер обратит внимание на худший возможный исход для каждой альтернативы, и он выберет максимум из минимумов («maximin»).
В рамках подхода Гурвица менеджер рассчитает «коэффициент оптимизма», как дробное значение α между 0 и 1, а затем будет стремиться максимизировать следующее выражение:
α*(лучший результат)+(1- α)*(худший результат).
В рамках подхода утраченных возможностей составляется матрица решений.
Таким образом, можно сделать вывод, что при принятии управленческих решений используются различные модели разработки и принятия управленческих решений. По мере увеличения степени неопределенности и риска повышается сложность и ответственность принятия управленческих решений. Наибольшая неопределенность и риск характерен для кризисных условий, поэтому принятие управленческих решений в условиях кризиса является наиболее проблематичным.
Библиографический список
1. A.J. Rowe, J.D. Boulgarides, Managerial Decision Making, Prentice-Hall, Englewood Cliffs, NJ, 1994.2. Dunn W.N. (1994). Public Policy Analysis: An introduction, New Jersey: Prentice Hall.
3. H.A. Simon, The New Science ofManagement Decision, Harper and Row, New York, 1960.
4. S.P. Robbins, Management, 6th edition, Prentice Hall, Engle¬wood Cliffs, NJ, 1999.