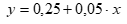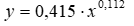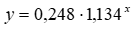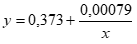Abstract: This article is devoted to determining the nature of the dependence of objective indicators for the formation of the concept of sustainable development of rural areas in the example of the Perm Territory. To perform the work, methods of system analysis were used to model the investigated object, as well as statistical methods for determining the quality of the interrelation of the indicators. The estimation of the received results is provided, the forecast is done.
Keywords: system model, initial system, correlation analysis, regression analysis, model quality estimation, forecast, forecast estimation.
В статье [1,стр. 202] была представлена модель зависимости показателей прироста социально-инженерного обустройства сельской местности Пермского края от прироста инвестиций в данную отрасль. Решение данного вопроса имеет приоритетное направление развития народного хозяйства [3, стр. 7]. Описанная в [1] модель была линейной регрессивной моделью, со значимыми показателями и хорошим критерием Фишера. В данной работе, на основе тех же данных, рассмотрим ряд нелинейных моделей.
Цель работы: методами системного анализа и статистики построить ряд моделей, описывающих зависимость ряда показателей социально-инженерного обустройства сельской местности Пермского края [2, стр. 665-696] от инвестиций в данную отрасль и выявить наиболее оптимальную, сделать прогноз.
- Модель системы.
Рассмотрим объект “Управление социально-инженерного обустройства сельскохозяйственной отрасли Пермского края”. Как известно из системного анализа, любой исследуемый объект может быть смоделирован и описан набором объективных свойств, характеризующих данный объект [4, стр. 169]. В [1, стр. 207] подробно изложен принцип и порядок моделирования рассматриваемой системы объекта. В статистических сводках [2, стр.665] в разделе “Социально-инженерное обустройство” были рассмотрены следующие показатели: 1) ввод в действие жилых домов в сельской местности, 2) ввод в действие общеобразовательных учреждений в сельской местности, 3) ввод в действие детских дошкольных учреждений в сельской местности, 4) ввод в действие учреждений культуры клубного типа в сельской местности, 5) ввод в действие водопроводных сетей в сельской местности, 6) ввод в действие газовых сетей в сельской местности, 7) ввод в действие автомобильных дорог в сельской местности, 8) ввод в действие линий электропередачи напряжением, 9) ввод в действие емкости телефонной сети в сельской местности.
Инвестирования в АПК идентифицируются по нескольким направлениям: инвестиции в основной капитал АПК (без учета лесного хозяйства), капитальные вложения за счет федерального бюджета (без учета лесного хозяйства), капитальные вложения за счет бюджетов субъектов Российской Федерации (без учета лесного хозяйства) [2, стр.61-70]. Так как выбранные показатели абсолютны и не характеризуют динамику изменения, был сделан перерасчет к показателям темпов прироста этих же показателей известными статистическими методами расчета временных рядов.
Таким образом, исходная система S исследуемого объекта описывается набором объективных свойств и параметров:
(1)
где 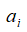 — имя свойства,
— имя свойства, 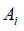 — множество проявлений этого свойства,
— множество проявлений этого свойства,  — имя базы системы,
— имя базы системы, 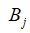 — множество проявлений базы [4, стр.. Свойства системы S совпадают с показателями прироста социально-инженерного обустройства и инвестирования, а проявления этих свойств, учитывая характер этих величин (темп прироста), являются числовыми и изменяются на отрезке [-1,1]. Параметрами системы S было решено считать две характеристики: время (год измерения) и группа. Все свойства объекта были разделены на две группы: группа “Социальное обустройство” и группа “инвестирование”. Все значения параметров базы также определились значениями измеренных показателей.
— множество проявлений базы [4, стр.. Свойства системы S совпадают с показателями прироста социально-инженерного обустройства и инвестирования, а проявления этих свойств, учитывая характер этих величин (темп прироста), являются числовыми и изменяются на отрезке [-1,1]. Параметрами системы S было решено считать две характеристики: время (год измерения) и группа. Все свойства объекта были разделены на две группы: группа “Социальное обустройство” и группа “инвестирование”. Все значения параметров базы также определились значениями измеренных показателей.
Поскольку цель исследования предполагала изучение влияния всей группы “Инвестирование” на группу “Социально инженерное обустройство” с учетом времени, было решено определить интегральный показатель для каждой из групп, представляющий из себя взвешенную сумму всех показателей, входящих в группу. Для определения весовых характеристик каждого свойства использовался широко известный метод анализа иерархий [5, стр. 154]. Таким образом, была получены значения интегральных показателей исходной системы S, представленные в таблице 1:
Таблица 1
Таблица значений интегральных показателей объекта
| Год | 2012 | 2013 | 2014 | 2015 |
| интегральный показатель темпов прироста инженерного обустройства местности | 0,2803 | 0,4712 | 0,528 | 0,215 |
| интегральный показатель темпов прироста инвестирования | 0,024 | 4,6396 | 6,326 | 0,0032 |
- Исследование влияния интегрального показателя инвестирования на показатель социально инженерного обустройства и определения оптимальной модели.
В работе [1, стр. 209] была построена линейная регрессионная модель, произведена оценка тесноты взаимосвязи методами корреляционно-регрессионного анализа [6, стр. 323], определена ошибка аппроксимации данной модели, вычислен коэффициент Фишера, что позволило сделать выводы о качестве модели. Был сделан прогноз изменения показателя социально-инженерного обустройства при увеличении интегрального показателя инвестирования на 5%. Определена ошибка и доверительный интервал прогноза. Прогноз оказался неточным.
В данной работе рассмотрим не только линейную модель, но и несколько нелинейных моделей [6, стр.383]: степенную модель 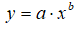 , показательную модель
, показательную модель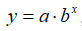 , гиперболическую модель
, гиперболическую модель 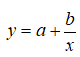 , где х – показатель прироста инвестирования, y – показатель прироста социально-инженерного обустройства. Определим все характеристики каждой модели и выберем оптимальную , используя индекс корреляции, коэффициент детерминации модели, критерий Фишера и среднюю ошибку аппроксимации.
, где х – показатель прироста инвестирования, y – показатель прироста социально-инженерного обустройства. Определим все характеристики каждой модели и выберем оптимальную , используя индекс корреляции, коэффициент детерминации модели, критерий Фишера и среднюю ошибку аппроксимации.
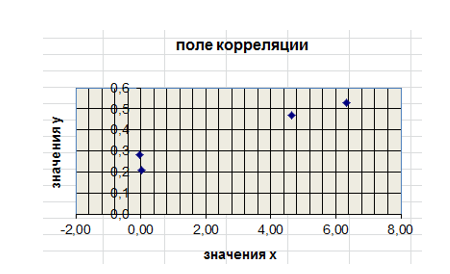
Поле корреляции показателей приведено на рисунке 1:
Рисунок 1.
После проведения необходимых расчетов, все полученные результаты выпишем в таблицу 2:
Таблица 2.
Таблица результатов.
| Параметры | Уравнение модели y=y(x) | Индекс корреляции ρYX | Коэффициент детерминации R2 | F-критерий Фишера | Средняя относительная ошибка Eотн |
| Модель | |||||
| Линейная | 0,98 | 0,96 | 54,13 | 1,96% | |
| Степенная | 0,99 | 0,98 | 158,02 | 0,75% | |
| Показательная | 0,97 | 0,95 | 37,9 | 2,3% | |
| Гиперболическая | 0,58 | 0,34 | 1,01 | 7% |
Как видно из таблицы 2, наиболее худшие результаты демонстрирует гиперболическая модель, к тому критерий Фишера, вычисленный по этой модели, составляет всего 1,01, что меньше табличного критического значения Fтабл=18,51. Так что данная модель вообще неприемлема для прогнозов. Все оставшиеся модели имеют примерно одинаковые характеристики, но большее значение F-критерия Фишера и большее значение коэффициента детерминации R2 имеет степенная модель. Она является оптимальной и ее можно взять в качестве лучшей для построения прогноза.
- Расчет прогнозного значения результативного показателя.
Учитывая характеристики степенной модели, сделаем прогноз: как изменится значение показателя темпов прироста социального обустройства, если темп прироста инвестирования увеличится на 5%? Используя уравнение регрессии степенной модели, можно сказать, что в этом случае показатель социального инженерного обустройства вырастет на 9,3%, при этом ошибка прогноза составляет 0,03 и предельное значение ошибки прогноза в 95% случаев не будет превышена 0,135. Доверительный интервал прогноза составляет [0,33; 0,61]. Диапазон верхней и нижней границ составляет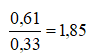 . Прогноз неточен, т.к. этот диапазон превышает пороговое значение точности: 1,85>1,5. Но стоит отметить, что этот показатель существенно снизился по сравнению с линейной моделью. Там он составил 4,264.
. Прогноз неточен, т.к. этот диапазон превышает пороговое значение точности: 1,85>1,5. Но стоит отметить, что этот показатель существенно снизился по сравнению с линейной моделью. Там он составил 4,264.
Выводы.
Несмотря на неточность прогноза, можно сказать, что есть существенное влияние темпов инвестирования на социальное обустройство сельского хозяйства. Также стоит увеличить объём выборки с учетом последующих лет. Учитывая неточности и погрешности в сборе статистических данных, в исследованиях временных рядов есть возможность применить методы регуляризации для понижения или устранения уровня шума, погрешности.
Библиографический список
1. Шилина А.В. Влияние инвестирования на социально инженерные показатели обустройства сельской местности на примере Пермского края за 2012-2015 гг. Сборник статей IV Международной научно-практической конференции.Пенза,2018. Издательство: "Наука и Просвещение", с. 207-211.2. Статистические таблицы. Агропромышленный комплекс России в 2015 году. – М.: Министерство Сельского хозяйства Российской федерации, 2016г. – 702с.
3. Кузнецова Э.Р., Мякшин Е.Н. Устойчивое развитие сельских территорий: теория, региональная практика. Пермь: ФГБОУ ВПО «Российская академия народного хозяйства и государственной службы при Президенте российской федерации» Пермский филиал, 2015. – 360с.
4. Миронов С.В., Пищухин А.М. Метасистемный подход в управлении.- Оренбург: ГОУ ОГУ, 2004.- 354 с.
5. Саати Т. Принятие решений, метод анализа иерархий. – М. “Радио и связь”, 1993г. – 278с.
6. Эконометрика: Учебник / Под ред. проф. В. Б. Уткина. — 2-е изд. — М.: Издательско-торговая корпорация «Дашков и К°», 2013 — 564 с.