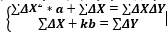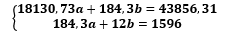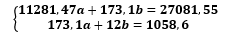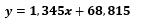Abstract: This article is devoted to the use of mathematical methods in Economics. Namely: calculation of the impact of investments on the growth of the gross regional product over time; calculation of the investment multiplier; calculation of the correlation coefficient. All calculations are based on statistical data from the Sverdlovsk and Chelyabinsk regions.
Keywords: The least-squares method, the Multiplier of Keynes, Coefficient of correlation, Chelyabinsk oblast, Sverdlovsk oblast
Введение
Уровень и перспективы экономического развития страны и отдельных субъектов федерации во многом зависят от инвестиционной деятельности. Конъюнктура инвестиционного рынка является основным фактором, определяющим динамику важнейших макроэкономических показателей. Очевидно, что без активной инвестиционной деятельности невозможно обеспечить требующиеся темпы роста валового внутреннего продукта и решение социальных задач. Необходимость увеличения объема инвестиций также обусловлена достаточно высоким уровнем износа основных фондов (на начало 2018 г. коэффициент износа по экономике в целом составлял 48,7%).
Наибольший удельный вес в общем объеме инвестиций в нефинансовые активы приходится на капитальные вложения (инвестиции в основной капитал – 98,6%). Именно эти инвестиции предопределяют состояние и эффективность деятельности реального сектора экономики.
Экономика и математика довольно сопряжённые науки. Как и любая научная дисциплина, экономическая теория использует ряд методов, в частности: метод наименьших квадратов, анализ значений мультипликатора Кейнса и коэффициент корреляции, помогающих специалистам решать поставленные задачи. Симбиоз данных наук позволит в разы увеличить динамику экономического роста страны и региона. Этим обуславливается важность и актуальность статьи.
Метод наименьших квадратов
Метод наименьших квадратов (МНК) был изобретён в первом десятилетии XIX века практически одновременно тремя учёными, два из которых – это математики А.М. Лежандр (1752-1833) [1] и К.Ф. Гаусс (1777-1855) [2]. В том же десятилетии на другом берегу Атлантики третий автор изобретения Р.А. Эдрейн (1775-1843) напечатал свой вывод нормального закона распределения вероятностей ошибок измерений и применил его «к установлению принципа наименьших квадратов» [3].
Н.Ш. Кремер в учебнике «Высшая математика для экономистов» давал следующее определение метода наименьших квадратов – это математический метод, применяемый для решения различных задач, точно отражающий общую тенденцию зависимости y от x, исключающий при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений [4].
На примере Свердловской и Челябинской областей мы можем применить данный метод, чтобы установить взаимосвязь изменений объемов инвестиций в основной капитал к изменению объемов Валового регионального продукта.
Имеются следующие данные Валового регионального продукта и объема инвестиций в основной капитал по Свердловской области [5] и по Челябинской области [6]:
Таблица 1
| Год | Свердловская | область | Челябинская | область |
| Инвестиции (в текущих основных ценах; миллионов рублей) | Сумма ВРП (в текущих основных ценах; миллионов рублей) | Инвестиции (в текущих основных ценах; миллионов рублей) | Сумма ВРП (в текущих основных ценах; миллионов рублей) | |
| 2006 | 133 476 | 653 908 | 89 200 | 446 918 |
| 2007 | 187 314 | 820 793 | 130 900 | 575 643,7 |
| 2008 | 242 634 | 923 551 | 181 006,3 | 664 492,7 |
| 2009 | 200 368 | 825 267 | 145 446,2 | 556 985,3 |
| 2010 | 264 462 | 1 046 600 | 151 121,5 | 652 865,5 |
| 2011 | 333 451 | 1 265 683 | 176 597,6 | 774 401,0 |
| 2012 | 341 635 | 1 484 879 | 192 816,4 | 841 972,3 |
| 2013 | 358 062 | 1 568 655 | 214 963,7 | 882 339,6 |
| 2014 | 371 631 | 1 659 784 | 227 860,6 | 993 900,6 |
| 2015 | 349 964 | 1 822 835 | 217 238,1 | 1 209 242,7 |
| 2016 | 328 403 | 1 990 837 | 198 289,2 | 1 271 133,1 |
| 2017 | 320 111 | 2 142 514 | 198 990,8 | 1 348 564,7 |
| 2018 | 318 008 | 2 250 000 | 259 365,6 | 1 505 600 |
Глядя на таблицу, можно сделать вывод, что пик по объёму инвестиций в Свердловской и Челябинской областях достигнут был в 2014 году.
Предполагая, что между переменными х и у существует линейная зависимость, найдем эмпирическую формулу вида y=ax+b, используя метод наименьших квадратов.
Также найдем необходимые для расчётов суммы. Промежуточные вычисления оформим в виде вспомогательной таблицы, где ΔX- инвестиции в миллиардах, ΔY- Валовый региональный продукт в миллиардах:
Таблица 2
| Свердловская область | Челябинская область | |||||||
| Год | * | * | ||||||
| 2006-2007 | 53,8 | 166,9 | 8979,22 | 2894,44 | 41,7 | 128,7 | 5 366,79 | 1 738,89 |
| 2007-2008 | 55,3 | 102,8 | 5684,84 | 3058,09 | 50,1 | 88,8 | 4 448,88 | 2 510,01 |
| 2008-2009 | -42,3 | -98,3 | 4158,09 | 1789,29 | -35,6 | -107,5 | 3 827 | 1 267,36 |
| 2009-2010 | 64 | 221,3 | 14163,2 | 4096 | 8,7 | 95,9 | 834,33 | 75,69 |
| 2010-2011 | 69 | 219 | 15111 | 4761 | 25,5 | 121,5 | 3 098,25 | 650,25 |
| 2011-2012 | 8,2 | 219,2 | 1797,44 | 67,24 | 16,2 | 67,6 | 1 095,12 | 262,44 |
| 2012-2013 | 16,4 | 83,8 | 1374,32 | 268,96 | 22,1 | 40,4 | 892,84 | 488,41 |
| 2013-2014 | 13,6 | 91,1 | 1238,96 | 184,96 | 12,9 | 111,6 | 1 439,64 | 166,41 |
| 2014-2015 | -21,7 | 163 | -3537,1 | 470,89 | -10,6 | 215,3 | -2 282,18 | 112,36 |
| 2015-2016 | -21,6 | 168 | -3628,8 | 466,56 | -19 | 61,9 | -1 176,1 | 361 |
| 2016-2017 | -8,3 | 151,7 | -1259,11 | 68,89 | 0,7 | 77,4 | 54,18 | 0,49 |
| 2017-2018 | -2,1 | 107,5 | -225,75 | 4,41 | 60,4 | 157 | 9 482,8 | 3 648,16 |
| ∑ | ∑184 | ∑1596 | ∑43 856,31 | ∑18 130,73 | ∑173,1 | ∑1 058,6 | ∑27 081,55 | ∑11 281,47 |
Исходя из данных таблицы, мы можем сказать, что активный рост инвестиций наблюдался до 2014 года. Именно в этот год курс рубля уменьшился по отношению к доллару вдвое, что сделала нашу страну и регионы инвестиционно-непривлекательными для иностранных контрагентов. И рост ВРП стал сокращаться с 2014 по 2018 год,
Система нормальных уравнений, применительно для Свердловской области, имеет вид:
Её решение a≈1,264; b≈113,587 даёт искомую зависимость:
𝒚=𝟏,𝟐𝟔𝟒𝒙+𝟏𝟏𝟑,𝟓𝟖𝟕
Система нормальных уравнений, применительно для Челябинской области, имеет вид:
Её решение a≈1,345; b≈68,815 даёт искомую зависимость:
Полученные в работе уравнения 𝒚=𝟏,𝟑𝟒𝟓𝒙+𝟔𝟖,𝟖𝟏𝟓; 𝒚=𝟏,𝟐𝟔𝟒𝒙+𝟏𝟏𝟑,𝟓𝟖𝟕 показывают, что с увеличением динамики инвестиций увеличивается динамика валового регионального продукта для Свердловской и Челябинской областях. Погрешность обуславливается небольшим количеством данных.
Мультипликатор Кейнса
Классическая кейнсианская теория утверждает, что существует так называемый «эффект мультипликатора инвестиций» [7], который заключается в том, что некоторое увеличение, прирост инвестиций приводит к значительно большему приросту валового внутреннего продукта (на региональном уровне — ВРП). Происходит это потому, что исходные инвестиции играют роль своеобразного толчка, увеличивающего спрос на инвестиционные товары, что приводит к росту производства и потребления соответствующих фирм, которые их производят. Они в свою очередь предъявляют спрос на продукцию смежных отраслей и т.д. В конце концов, рост занятости и доходов вызывает увеличение производства в отраслях, производящих потребительские товары.
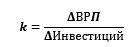
На примере двух областей и используя статистические данные из прошлой главы мы будем рассчитывать коэффициент, показывающий, во сколько раз возрастет ВРП при увеличении инвестиций – то есть — Мультипликатор инвестиций. По следующей формуле:
Полученные результаты оформим таблицей:
Таблица 3
| Года | Свердловская область | Челябинская область | |
| 2006-2007 | 3,1 | 3 | |
| 2007-2008 | 1,86 | 1,8 | |
| 2008-2009 | 2,3 | 3 | |
| 2009-2010 | 3,5 | 11 | |
| 2010-2011 | 3,2 | 4,8 | |
| 2011-2012 | 26,7 | 4,2 | |
| 2012-2013 | 5,1 | 1,8 | |
| 2013-2014 | 6,7 | 8,7 | |
| 2014-2015 | -7,5 | -20,3 | |
| 2015-2016 | -7,8 | 3,3 | |
| 2016-2017 | -18,3 | 110,6 | |
| 2017-2018 | -53,7 | 2,6 | |
После расчётов наблюдается парадокс, потому что понижение объемов инвестиций даёт увеличение объемов ВРП, как в Свердловской области, так и в Челябинской. Объяснение этому может быть юридический фактор, когда предприятие ведет деятельность на территориях Челябинской и Свердловской областях, а зарегистрирована в Москве.
Коэффициент корреляции
Корреляция, или корреляционная зависимость — статистическая взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин [8].
Произведем расчёты используя статистические показатели Свердловской и Челябинской областях. Результаты оформим таблицей:
Таблица 4
| № | Челябинская область | Свердловская область | ||
| Δx | Δy | Δx | Δy | |
| 1 | 41,7 | 128,7 | 53,8 | 166,9 |
| 2 | 50,1 | 88,8 | 55,3 | 102,8 |
| 3 | -35,6 | -107,5 | -42,3 | -98,3 |
| 4 | 8,7 | 95,9 | 64 | 221,3 |
| 5 | 25,5 | 121,5 | 69 | 219 |
| 6 | 16,2 | 67,6 | 8,2 | 219,2 |
| 7 | 22,1 | 40,4 | 16,4 | 83,8 |
| 8 | 12,9 | 111,6 | 13,6 | 91,1 |
| 9 | -10,6 | 215,3 | -21,7 | 163 |
| 10 | -19 | 61,9 | -21,6 | 168 |
| 11 | 0,7 | 77,4 | -8,3 | 151,7 |
| 12 | 60,4 | 157 | -2,1 | 107,5 |
| 0,490306 | 0,534886 | |||
| tнабл | 1,778994 | 2,001903 | ||
| tкр(0,05; 10) | 2,228139 | 2,228139 | ||
Интуитивно подразумевается, что чем больше инвестиций, тем больше должен быть и ВРП. Однако расчеты коэффициента корреляции показывают, что такой взаимосвязи нет.
Заключение
Произведя все расчеты, мы наблюдаем такую ситуацию, когда математические законы не работают для прогнозирования и анализа реального экономического положения в Свердловской и Челябинской областях. Много факторов остается за рамками имеющейся информации, изменения ВРП могут быть связаны с разными факторами (например, юридической привязкой: организации находятся на территории этих областей, а зарегистрированы в Москве, либо вкладывали в капитал на протяжении долгих лет, отдача наблюдается во время понижений инвестиций и др.).
Библиографический список
1. Legendre A.M. Nouvelles méthodes pour la détermination des orbites des cometes; avec un supplément contenant divers perfectionnemens de ces methodes et lauf application aux deux comètes de 1803. Paris, Courcier, 1806.2. Гаусс К.Ф. Избранные геодезические сочинения. т.1. Под редакцией, с введением и комментариями Г.В.Багратуни. – М., Геодиздат, 1958. – 152 с.
3. Adrian R. Research concerning the probabilities of the errors which happen in making observations. – The analyst or mathematical museum. – Philadelphia, 1908, V. 1, N 4, p. 93 – 109.
4. Кремер Н.Ш. Высшая математика для экономистов [Текст]/Понятие об эмпирических формулах. Метод наименьших квадратов. Под редакцией профессора Кремер Н.Ш. , 2007. – С. 425-430
5. Статистика валового регионального продукта [Электронный ресурс]/: Управление Федеральной службы государственной статистики по Свердловской области и Курганской области. Режим доступа: https://sverdl.gks.ru/folder/29700
6. Статистика валового регионального продукта и объема инвестиций [Электронный ресурс]/: Федеральная служба государственной статистики. Режим доступа: https://chelstat.gks.ru/storage/mediabank/INVEST.pdf
7. Кейнс Дж. М. Общая теория занятости, процента и денег. — М.: Эксмо, 2007 — 960 с.
8. Общая теория статистики: Учебник / Под ред. Р. А. Шмойловой. — 3-е издание, переработанное. — Москва: Финансы и Статистика, 2002. — 560 с. — ISBN 5-279-01951-8.