1.  ВВЕДЕНИЕ

Ценовая эластичность непосредственно характеризует чувствительность спроса к цене; знание ее величины помогает рассчитать уровень спроса для различных цен. Однако на практике определить и рассчитать эластичность конкретного товара представляется трудной задачей ввиду отсутствия данных или неточности информации. Один из методов определе-ния ценовой эластичности заключается в построении экономико-математических моделей. Моделирование поведения потребителей на рынке, установление формульных зависимостей и взаимосвязей многих психологических и социальных факторов представляет достаточно трудную задачу, но в случае ее успешного решения, как правило, дает ощутимые результаты.
В модели экономического равновесия 4] представлены экономические силы спроса   и предложения   Эти формулы соответственно имеют вид:

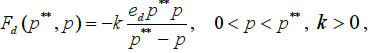                                      (1)

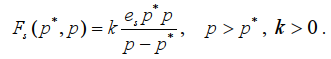                                              (2)

Здесь использованы следующие обозначения:
e_d — абсолютная величина коэффициента эластичности спроса по цене;
e_s —  абсолютная величина коэффициента эластичности предложения по цене;
k — коэффициент пропорциональности, зависящий от  специфики реализуемого товара или услуги на рынке;
p — текущая цена единицы товара;
p⁰ -  равновесная цена товара;
p* — нижнее пороговое значение цены товара, связанное с осуществленными затратами со стороны продавца;
p** —  верхнее потолочное значение цены товара, выше которого покупатели отказываются приобретать предлагаемый товар;
P =p** —  p* —  длина интервала допустимых цен .
В цитируемой работе 4 равновесие рынка находится из равенства абсолютных величин рыночных сил (1) и (2). Поэтому приходим к следующему уравнению равновесной цены :

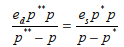                                                                                                             (3)

при условии, что

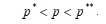                                        .                                                                            (4)

Формула эластичности спроса. Решая уравнение (3), находим выражение для параметра ценовой эластичности спроса в виде

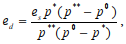                                                                                                         (5)

определенное соотношением (4), то есть равновесие принадлежит интервалу допустимых цен рынка. Поставим цель исследовать поочередно свойства функции (5).

2.   ЗАВИСИМОСТЬ  ЦЕНОВОЙ  ЭЛАСТИЧНОСТИ  СПРОСА ОТ  ПАРАМЕТРА

Свойства функции 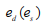. Из формулы (5) видно, что эластичность спроса по цене e_d является линейной возрастающей функцией эластичности предложения по цене e . Кроме то-го, имеем предельное равенство:

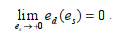                                                                                                                 (6)

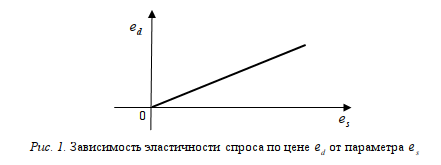
На основании отмеченных свойств функции 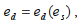определяемой формулой (5) и (6), схема ее графика изображена на рис. 1. Здесь линия графика представляет некоторую часть прямой, определяемую экономическими условиями модели.

Эластичность функции e_d по параметру e_s. Для исследования эластичности положим x=e_s. Тогда из равенства (5) получим функцию

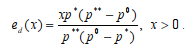                                                                                          (7)

Воспользуемся общепринятым в экономике способом вычисления эластичности E(e_d(x)) для непрерывно дифференцируемой функции e_d(x). Она определяется формулой:

.

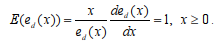Таким образом, E(e_d(x))=1, или имеет место единичная эластичность. Это означает, что рассматриваемый параметр   растет теми же темпами, что и воздействующий на него фактор  e_s.

3.   ЗАВИСИМОСТЬ  ОТ  ГРАНИЦ  ИНТЕРВАЛА  ДОПУСТИМЫХ  ЦЕН

Преобразуем формулу (5), записав ее в виде функций 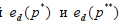 зависимостей соответственно от параметров нижней пороговой границы p*  и верхней потолочной границы p** интервала допустимых цен. Тогда получим следующие выражения:

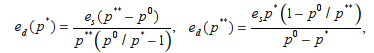                            (8)

Из формул (8) видим, что эластичность спроса по цене e_d  является возрастающей функцией параметров p* и  p**, причем первая из функций определена для значений  p* из интервала 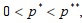а вторая — для значений p**, подчиненных неравенству 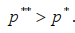Справедливы следующие предельные условия:

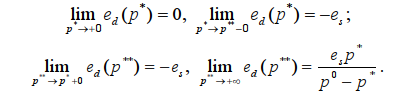
Кроме того, нетрудно проверить, что вторая производная функции 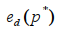 положительна при

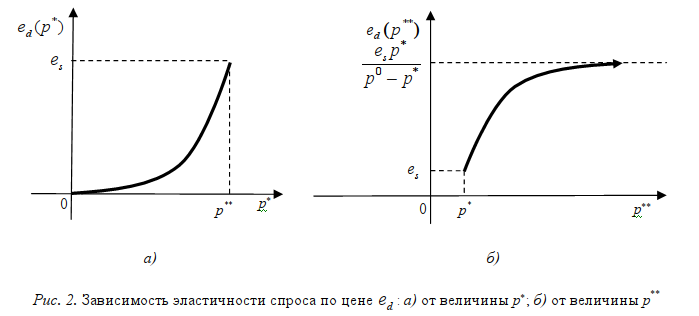
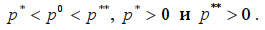Следовательно, функция является выпуклой. Вторая производная другой функции e_d(p**)  отрицательна при   p*>0 и  p**>0, что значит, что данная функция является вогнутой. Пользуясь формулами (8), можно изобразить схемы графиков двух функций  e_d=e_d(p*) и e_d=e_d(p**)   (рис. 2).

Эластичность функции e_d  по параметрам p*  и p**. Исследуем эластичность функции  e_d относительно каждой из границ интервала допустимых цен. Положим x = p*, тогда для первого из равенств (8) получим функцию

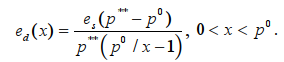
Вычисляя эластичность функции e_d(x)  в зависимости от x, после необходимых преобразований получим:

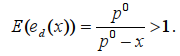
Положим теперь y = p**, тогда для второго из равенств (8) получим функцию

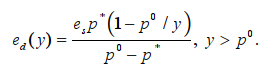
Здесь эластичность E(e_d(y))   функции по отношению к y представляется следующим выражением:

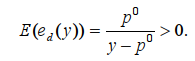
Простые рассуждения приводят к следующим выводам:

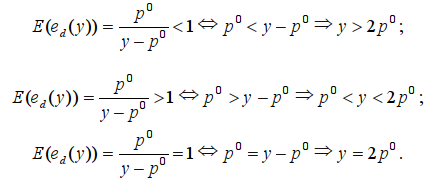
Схемы графиков функций эластичностей E(e_d(p*)) и E(e_d(p**)) представлены на рис. 3.

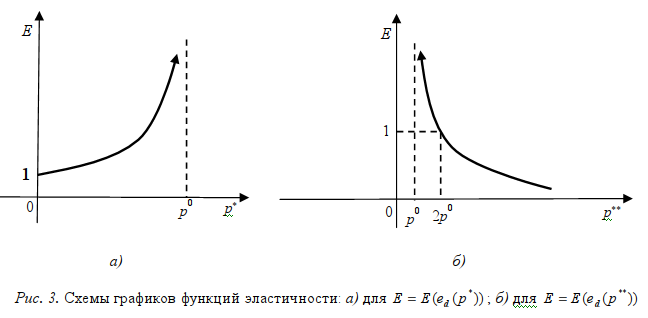
Таким образом, функция e_d  эластична по нижней границе интервала допустимых цен p* и имеет различную эластичность в зависимости от значения равновесной цены p⁰ по верхней границе интервала допустимых цен  p**.

4.   ЗАВИСИМОСТЬ  ОТ  РАВНОВЕСНОЙ  ЦЕНЫ

Преобразуем формулу (5), записав ее в виде функции  e_d(p⁰)  зависимости от параметра равновесной цены рынка. Тогда получим следующее выражение:

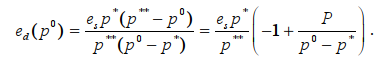                             (9)

Из формулы (9) видим, что эластичность спроса по цене e_d является убывающей функцией параметра p⁰, причем функция определена для значений p⁰ из интервала p*<p⁰<p**.  Справедливы следующие условия:

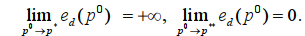
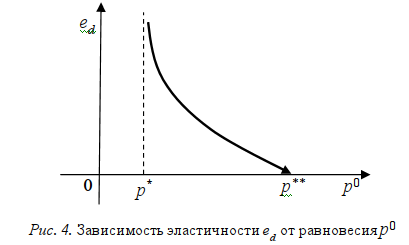
Кроме того, вторая производная функции e_d(p⁰) положительна при p⁰>0. Следовательно, функция является выпуклой. Пользуясь формулой (9), можно изобразить схему графика функции   e_d =  e_d(p⁰) (рис. 4).

Эластичность по параметру равновесия. Согласно формуле (5) имеем функцию

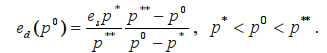                                         (10)

Она дробно-линейная, ее функция эластичности вычисляется по приведенной формуле. В результате получим: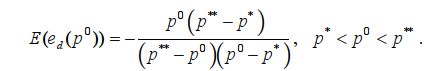

Вычислим производную функции  E(e_d(x)), где  x=p⁰.  Имеем:

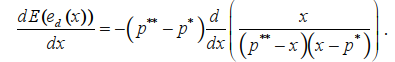
Вычисляем выражение

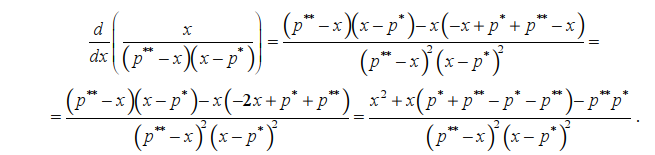
Следовательно, возвращаясь к исходному обозначению  x = p⁰, получаем:

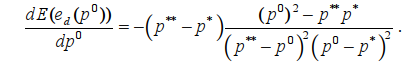                      (11)

Анализируя формулу (11), приходим к выводу, что функция   имеет глобальный максимум на интервале своего определения в точке

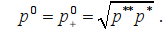
В этой точке E(е_d(p₊⁰))   принимает значение, равное

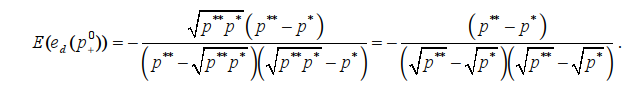
После упрощения получим:

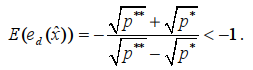                                                               (12)

Кроме того, имеют место предельные равенства:

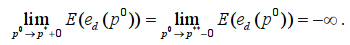                                    (13)

В соответствии со свойствами (12) и (13) схема графика функции (11) представлена на рис. 5.

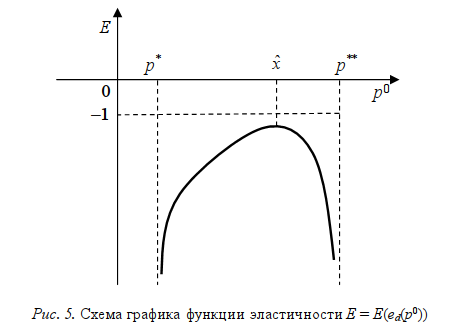
Неравенство (12) и равенства (13) показывают, что величина e_d  эластична по параметру равновесия  p⁰.

5.   ЗАКЛЮЧЕНИЕ

Экономико-математическая модель эластичности спроса по цене e_d построена на основании формулы экономического равновесия, разработанного авторами. Анализ модели взаимодействия экономических сил спроса и предложения с целью установления формулы ценовой эластичности спроса осуществляется на заранее заданном интервале p*<p<p** допустимых цен рынка. Выражение для e_d представлено в виде функциональной зависимости от рыночного равновесия p⁰, ценовой эластичности предложения e_s и граничных значений p*, p** интервала допустимых цен. Формула (5) позволяет выяснить потенциальные возможности вычисления эластичности спроса по цене при других заданных параметрах модели равновесия. По результатам исследования можно отметить следующие свойства.

1)    Эластичность спроса по цене e_d  является линейной возрастающей функцией эластичности предложения по цене e_s, при этом имеет место единичная эластичность.  Это означает, что параметр e_d растет теми же темпами, что и воздействующий на него фактор e_s .
2)    Эластичность спроса по цене  e_d, как функция нижней границы интервала допустимых цен рынка  p* (0<p*<p**), возрастает с ростом параметра p*, т. е. с увеличением нижнего порогового значения цены товара, связанного с осуществленными затратами со стороны продавца, ценовая эластичность спроса увеличивается. Зависимость e_d=e_d(p*) является возрастающей выпуклой функцией.
3)    Эластичность спроса по цене  e_d, как функция верхней потолочной границы интервала допустимых цен   p** (p**>p* ), возрастает с ростом параметра p**, т. е. с увеличением верхнего потолочного значения цены товара, выше которого покупатели отказываются приобретать предлагаемый товар, ценовая эластичность спроса также увеличивается. Зависимость e_d=e_d(p**) является возрастающей вогнутой функцией.
4)    Функция  e_d эластична по нижней границе интервала допустимых цен p*, однако имеет различную эластичность в зависимости от значения равновесной цены  p⁰ по верхней границе интервала допустимых цен  p**.
5)    Эластичность спроса по цене e_d  является убывающей выпуклой функцией параметра  равновесной цены p^o  допустимого интервала цен p*<p⁰<p** и эластична по данному параметру.
6)    Функция эластичности E(e_d(p⁰))   отрицательна, обладает глобальным максимумом и убывает на интервале p*<p⁰<p**.