Abstract: The article uses the method of correlation-regression modeling for constructing a portrait of the consumer of a firm. Construct a multifactor regression model that best describes the dependence of indicators characterizing the consumer (supplier, competitor, sponsor, etc.) using the Statistica package. The semantic interpretation of the results is given, the importance of the resultant indicator of the business activity is predicted, and on the basis of the conclusions it is proposed to propose a system of marketing activities that stimulate business.
Keywords: consumer portrait, correlation-regression method, regression, multifactor model, dependent variable
Введение
Региональный благотворительный центр поддержки и организации досуга тяжелобольных детей и детей-сирот изучает портрет спонсора, в основе которого лежит зависимость размера спонсорской (благотворительной) помощи от девяти факторов: вид оказываемой помощи (материальная (Х1), досуговая (Х2), транспортная (Х3), вещественная (Х4), другая (Х5)), возраст (Х6), организационно-правовая форма лица, оказывающего помощь (Х7), уровень дохода спонсора (благотворителя) — (Х8-Х11), и периодичность оказания помощи центру (Х12).
Требуется построить линейную регрессионную модель с фиктивными переменными для качественных показателей:
Рисунок 1. Фиктивные переменные
На основе полученной модели требуется спрогнозировать размер оказываемой помощи благотворителем – физическим лицом в возрасте 50 лет с уровнем дохода свыше 30000 рублей, оказывающем материальную помощь в среднем один раз в месяц.
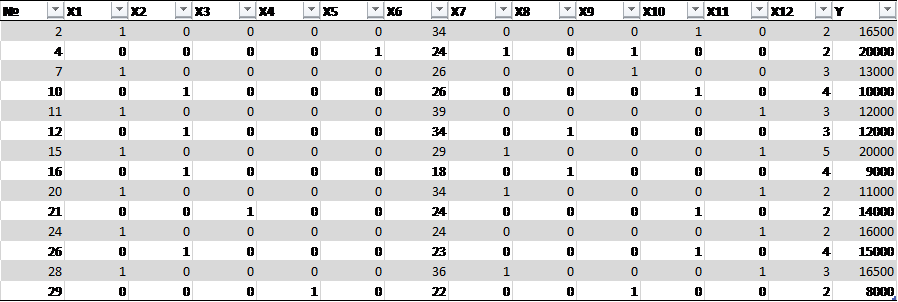
Источник данных: Результаты анкетирования 30 благотворителей, сотрудничающих с Региональным благотворительным центром поддержки и организации досуга тяжелобольных детей и детей-сирот (респондентов отбирали методом случайного бесповторного отбора из числа постоянных спонсоров благотворительной организации).
Рисунок 2.Исходные данные
Объекты и методы исследования
Объектами исследования выступили благотворители, сотрудничающие с Региональным благотворительным центром поддержки и организации досуга тяжелобольных детей и детей-сирот. Для проведения исследования был применет корреляционно-регрессионный метод.
Экспериментальная часть
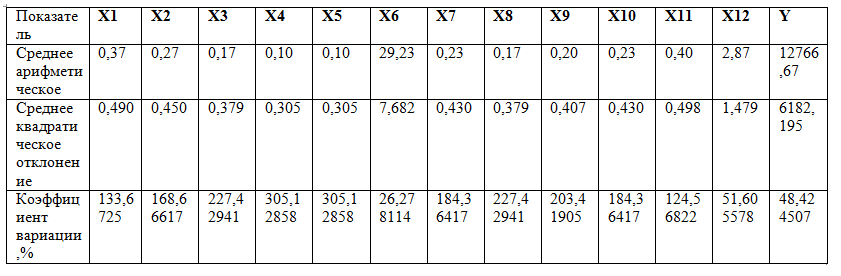
1.На этапе дискриптивно-статистического анализа определяются значения средних величин, средних квадратических отклонений, значения коэффициентов асимметрии, эксцесса и их среднеквадратические ошибки по результативному и факторным признакам.
Таблица 1
Статистический анализ
| Variable | Descriptive Statistics (Spreadsheet2) | ||||||||||||||||
|
|
|
|
|
|
|
|
| |||||||||
| 30 | 0,37 | 0,000 | 1,00 | 0,490 | 0,582933 | 0,426892 | -1,78401 | 0,832746 | ||||||||
| 30 | 0,27 | 0,000 | 1,00 | 0,450 | 1,111663 | 0,426892 | -0,82386 | 0,832746 | ||||||||
| 30 | 0,17 | 0,000 | 1,00 | 0,379 | 1,884415 | 0,426892 | 1,65714 | 0,832746 | ||||||||
| 30 | 0,10 | 0,000 | 1,00 | 0,305 | 2,809120 | 0,426892 | 6,30805 | 0,832746 | ||||||||
| 30 | 0,10 | 0,000 | 1,00 | 0,305 | 2,809120 | 0,426892 | 6,30805 | 0,832746 | ||||||||
| 30 | 29,23 | 16,000 | 47,00 | 7,682 | 0,287253 | 0,426892 | -0,36160 | 0,832746 | ||||||||
| 30 | 0,23 | 0,000 | 1,00 | 0,430 | 1,328338 | 0,426892 | -0,25732 | 0,832746 | ||||||||
| 30 | 0,17 | 0,000 | 1,00 | 0,379 | 1,884415 | 0,426892 | 1,65714 | 0,832746 | ||||||||
| 30 | 0,20 | 0,000 | 1,00 | 0,407 | 1,580130 | 0,426892 | 0,52745 | 0,832746 | ||||||||
| 30 | 0,23 | 0,000 | 1,00 | 0,430 | 1,328338 | 0,426892 | -0,25732 | 0,832746 | ||||||||
| 30 | 0,40 | 0,000 | 1,00 | 0,498 | 0,430057 | 0,426892 | -1,94996 | 0,832746 | ||||||||
| 30 | 2,87 | 1,000 | 6,00 | 1,479 | 0,518743 | 0,426892 | -0,49021 | 0,832746 | ||||||||
| 30 | 12766,67 | 2000,000 | 25000,00 | 6182,195 | 0,077946 | 0,426892 | -0,77958 | 0,832746 | ||||||||
Сравнивая значения средних величин и их средних квадратических отклонений – определим коэффициенты вариации (отношение ср. кв. отклонения и ср. арифметического) по всем факторам (таблица 2). Анализ полученных коэффициентов вариации свидетельствует о повышенном уровне варьирования факторов.
Таблица 2
Коэффициенты вариации
Таким образом, совокупность исследуемых факторов неоднородна, а их средние значения – нетипичны. Это обстоятельство не позволяет использовать исходные данные в дальнейшем анализе. Необходимо провести корректировку исходных данных, чтобы снизить значения коэффициентов вариации до 35%.
Анализ коэффициентов асимметрии и эксцесса позволяет сделать следующие выводы. Для факторов X6,X12,Y наблюдается правосторонняя асимметрия (коэффициент асимметрии больше 0). Для всех количественных факторов ряды распределения данных плосковершинны (коэффициент эксцесса меньше 0). Это свидетельствует об отсутствии близости распределений факторов к нормальному закону.
Таким образом, чтобы применить метод корреляционно-регрессионного моделирования, требуется корректировка данных (для снижения уровня вариации факторов и приведения распределений факторов к распределению близкому к нормальному закону).
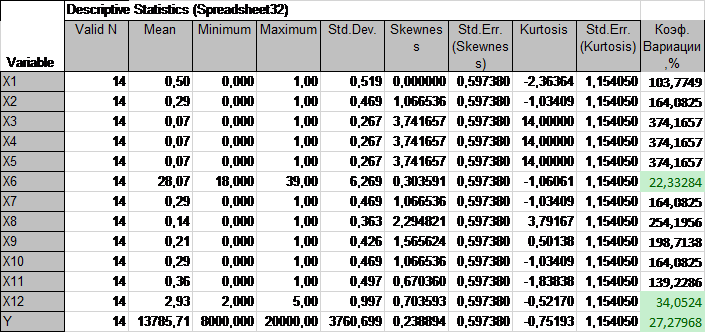
Рисунок 3. Исходные данные в процессе корректировки
Рисунок 4. Заключительный дескриптивно-статистический анализ
Сокращение вариации факторов позволило получить однородные данные для факторов X6,X12,Y и значительно снизить вариацию для остальных факторов. В результате корректировки данных удалось довести значения коэффициентов асимметрии и эксцесса до требуемых уровней (<|1|). Это позволяет сделать вывод о близости распределений всех факторов к нормальному закону.
Таким образом, по итогам дескриптивно-статистического анализа делается заключительный вывод о возможности применения метода корреляционно-регрессионного моделирования для дальнейшего исследования.
2.Построение уравнения множественной регрессии
Результаты работы модуля множественная регрессия:
Dependent: Var10 Множ. R = 0 ,80100921 F = 0,1491918
R2= 0,64161575 df = 12,1
No. of cases: 14
Скорректированная R2= -3,6589953 p = ,976297
Стандартная ошибка оценки:8117,3582166
Свободный член: 11639,542983 Стандартная ошибка: 19941,13 t( 1) =0 ,58370 p = 0,6636
X1 b*=,211 X5 b*=-,38 X9 b*=-,01
X2 b*=-,22 X6 b*=,485 X10 b*=-,07
X3 b*=,159 X7 b*=-,03 X11 b*=-,14
X4 b*=,196 X8 b*=-,04 X12 b*=,252
По полученным результатам можно дать следующие оценки модели:
1.Значение множ. коэф. корреляции Rух1х2х3х4х5х6х7x8x9x10x11x12= 0,8 свидетельствует о наличии достаточно тесной связи между (У) и факторами (Х1, Х2, Х3, Х4, Х5, Х6, Х7,X8,X9,X10,X11,X12).
2.Значение коэффициента множественной детерминации R2= 0,64 свидетельствует о том, что факторы Х1, Х2, Х3, Х4, Х5, Х6, Х7,X8,X9,X10,X11,X12 на 64% характеризуют изменчивость результата Y. Это значит, что модель не учитывает 36% факторов, влияющих на Y.
Таблица 3
Итоговая таблица регрессии
| N=14 | Ridge Regression Summary for Dependent Variable: Var10 (Spreadsheet3) l=,10000 R= ,80100921 R?= ,64161575 Adjusted R?=-3,6589953 F(12,1)=,14919 p | ||||||||||
|
|
|
|
|
| ||||||
| 11639,54 | 19941,13 | 0,583695 | 0,663645 | |||||||
| 0,210997 | 1,307403 | 1529,26 | 9475,80 | 0,161386 | 0,898137 | |||||
| -0,382606 | 1,317992 | -3069,21 | 10572,73 | -0,290295 | 0,820136 | |||||
| -0,006761 | 0,862689 | -95,13 | 12139,11 | -0,007837 | 0,995011 | |||||
| -0,217188 | 0,905040 | -3056,11 | 12735,04 | -0,239976 | 0,850062 | |||||
| 0,485446 | 0,995174 | 6830,82 | 14003,33 | 2,487800 | 0,711076 | |||||
| -0,069899 | 0,750101 | -41,93 | 449,97 | -0,093186 | 0,940847 | |||||
| 0,159422 | 0,830445 | 1278,86 | 6661,70 | 1,191972 | 0,879256 | |||||
| -0,027217 | 1,040400 | -281,86 | 10774,54 | -0,026160 | 0,983350 | |||||
| -0,144669 | 1,163465 | -1277,69 | 10275,44 | -0,124344 | 0,921245 | |||||
| 0,195748 | 1,155714 | 1570,26 | 9270,96 | 0,169374 | 0,893187 | |||||
| -0,040789 | 1,249355 | -308,49 | 9448,96 | -0,032648 | 0,979223 | |||||
| 0,251985 | 0,770387 | 950,25 | 2905,19 | 2,327088 | 0,798752 | |||||
В графе В приведены коэффициенты регрессии, на основании которых строим многофакторную регрессионную модель: У =11639,54+ 1529,26X1-3069,21X2-95,13X3 -3056,11X4+6830,82X5-41,93X6+1278,86X7-281,86X8-1277,69X9+1570,26X10-308,49X11+950,25X12
Полученная модель может быть уточнена, поскольку не все коэффициенты регрессии проходят проверку на критерий Стьюдента с вероятностью большей 95%. Расчетные значения t-критериев Стьюдента представлены в графе t(3), а вероятности ошибки, с которыми эти критерии были рассчитаны – в графе p-level. Табличное значение t-критерия Стьюдента при вероятности 95%, уровне значимости α=0,05 (5%) и числе степеней свободы df=13 определяем по таблице tтаб = 2,1604. Проведем проверку на t-критерий Стьюдента :
| t рас | = 0,583695<t таб (2,1604) — для свободного члена ао;
| t рас | = 0,161386<t таб (2,1604) — для коэффициента а1;
| t рас | = 0,290295<t таб (2,1604) — для коэффициента а2;
| t рас | = 0,007837< t таб (2,1604) — для коэффициента а3;
| t рас | =0,239976< t таб (2,1604) — для коэффициента а4;
| t рас | =2,487800> t таб (2,1604) — для коэффициента а5 ;
| t рас | = 0,093186< t таб (2,1604) — для коэффициента а6;
| t рас | = 1,191972< t таб (2,1604) — для коэффициента а7;
| t рас | = 0,026160< t таб (2,1604) — для коэффициента а8;
| t рас | = 0,124344< t таб (2,1604) — для коэффициента а9;
| t рас | = 0,169374< t таб (2,1604) — для коэффициента а10;
| t рас | = 0,032648< t таб (2,1604) — для коэффициента а11;
| t рас | = 2,327088> t таб (2,1604) — для коэффициента а12;
ВЫВОД. Таким образом, с вероятностью большей 95% статистически значимыми коэффициентами регрессии являются а5, а12, остальные коэффициенты сформированы под влиянием случайных причин. Поэтому факторы Х1, Х2, Х3, Х4,X6,Х7,X8,X9,X10,X11 можно исключить из модели как малоинформативные.
3.Построение двухфакторной модели
Построим уточненную двухфакторную модель. Затем проверим ее качество и то, насколько характеристики новой двухфакторной модели будут отличаться от первого варианта – 2-ти факторной модели.
Результаты множественной регрессии
Dependent: Var13 Множественная регрессия R = 0,50886563 F = 1,921844
R2= ,25894423 df = 2,11
Число наблюдений: 14 скорректирован. R2= 0 ,12420681 p = ,192389
Стандартная ошибка оценки:3519,4059085
Intercept: 11182,692308 Std.Error: 3200,383 t( 11) = 3,4942 p = 0 ,0050
X5 b*=0,526 X12 b*=0,188
Таблица 4
Двухфакторная модель (итоговая таблица регрессии)
| N=14 | Regression Summary for Dependent Variable: Var13 (Spreadsheet35) R= ,50886563 R2= ,25894423 Adjusted R2= ,12420681 F(2,11)=1,9218 p | ||||||||||
|
|
|
|
|
| ||||||
| 11182,69 | 3200,383 | 3,494173 | 0,005022 | |||||||
| 0,525941 | 0,269410 | 7400,64 | 3790,935 | 1,952194 | 0,076830 | |||||
| 0,187833 | 0,269410 | 708,33 | 1015,965 | 0,697203 | 0,500146 | |||||
Двухфакторная регрессионная модель примет вид: Y=11182,69+7400,64X5+708,33X12
4.Построение моделей парной и частной корреляции
Таблица 5
Матрица парных корреляций
| Переменная | Correlations (Spreadsheet40) Marked correlations are significant at p < ,05000 N=14 (Casewise deletion of missing data) | ||||
|
|
| |||
| 1,000000 | 0,046882 | 0,475602 | ||
| 0,046882 | 1,000000 | -0,267999 | ||
| 0,475602 | -0,267999 | 1,000000 | ||
Полученные значения парных коэффициентов корреляции свидетельствуют о наличии хорошей положительной связи между размером спонсорской помощи (У) и периодичностью оказания помощи центру (Х12) – ryx5=0,47 , а также о наличии слабой положительной связи между другим видом помощи(Х12) – ryx12=0,05. При этом отсутствие межфакторной связи rx5x12= -0,27 положительно построенную регрессионную модель.
Таблица 6
Частные корреляции
| Variable | Variables currently in the Equation; DV: Var13 (Spreadsheet45) | ||||||||||||
|
|
|
|
|
|
| |||||||
| 0,187833 | 0,205718 | 0,180962 | 0,928177 | 0,071823 | 0,697203 | 0,500146 | ||||||
| 0,525941 | 0,507259 | 0,506701 | 0,928177 | 0,071823 | 1,952194 | 0,076830 | ||||||
Значения которых: rух12/ х5 = 0,5;rух5/ х12 = 0,2 , подтверждают наличие умеренно-тесной положительной связи между размером спонсорской помощи (У) и периодичностью оказания помощи центру (Х12) (исключая влияние Х5), а также умеренной положительной связи между размером помощи(У) и другими видами помощи (Х5) (исключая влияние Х12), с высокой степенью вероятности р>95%.
Оценим статистическую надежность полученного уравнения множественной регрессии с помощью общего F-критерия Фишера, который проверяет нулевую гипотезу о статистической незначимости параметров построенного регрессионного уравнения и показателя тесноты связи (Но: а0=а12=а5=0, Rух12х5 =0).
Фактическое значение F-критерия Фишера – Fрас= F = 1,921844 сравниваем с табличным значением – Fтаб= 3,98. Поскольку Fрас< Fтаб, то гипотеза Но подтверждается.
Полученные результаты свидетельствуют о том, что анализируемые данные ненадежно доказывают наличие линейной связи между результатом и факторами. Признается статистическая ненадежность полученного регрессионного уравнения в целом, а также параметров регрессии а0, а12 и а5 и показателя тесноты связи Rух12х5.
Сама модель Y=11182,69+7400,64X5+708,33X12 может быть интерпретирована следующим образом. С увеличением частоты оказания помощи на 1, размер помощи возрастает на 7400,6 рублей. При увеличении других видов помощи на 1, размер оказываемой помощи увеличивается на 708,33. (при неизменности первого включенного в модель фактора).
Заключение
Точечный и интервальный прогноз с вероятностью 95% по следующим данным: Х1= 0; Х2= 0; Х3=0; Х4=0; Х5= 0; Х6= 50; Х7=0;X8=0;X9=0;X10=0;X11=1;X12=1
Подставляя в модель планируемые значения можно построить точечный прогноз спроса:
У* = 11639,54+1529,26X1-3069,21X2-95,13X3-3056,11X4+6830,82X5-41,93*50+1278,86X7-281,86X8-1277,69X9+1570,26X10-308,49*1+950,25* 1=10185руб.
Но поскольку не все показатели признаны значимыми, правильнее будет рассчитать прогноз по новой модели:
У = 11182,69+7400,64X5+708,33X12
У* = 11182,69+708,33=11891 руб.
Для построения доверительного интервала: y**ϵ[У*±Δ *] необходимо определить tтабл (по таблицам t-критерия Стьюдента) и Ϭ.
tтабл= 2,1604; Ϭ=11891/1,39(корень из F) =8554,7; Δ *= 2,1604*8554,7=18481,5.
Таким образом, интервальный прогноз c вероятностью 95% составит:
y**ϵ[11891-18481,5.; 11891+18481,5], т.е. y**ϵ[-6590,5;30372,5].
Библиографический список
1. Лапыгин Ю.Н., Крылов В.Е., Чернявский А.П. Экономическое прогнозирование: учебное пособие. Гриф УМО - М.: Эксмо, 2009, - 256 с.2. Лукьянова Н.Ю. Статистический анализ данных с использованием компьютера: Учебное пособие. Грифы ведомственные и УМО - Калининград: Изд-во КГУ, 2003. – 88с.