Abstract: The author has offered creation of mathematical model of trade of the Russian Federation on the basis of Solow's model. Considering a variety of production functions of Solow and and also discretization and the continuity of time, the author has combined six various mathematical models of trade of the Russian Federation. Taking into account specifics of branch of trade the author has added restriction on final consumption. Also the author has suggested to apply production function of Cobb-Douglas in Solow's model.
Keywords: Mathematical model, production function, work, capital, differentiation, discrete time.
Актуальность. Математическая модель объекта исследования позволяет определить внутренние закономерности, присущие данному объекту и спрогнозировать поведение объекта исследования. Разумеется, относительно заранее выбранных свойств объекта исследования.
Объект исследования – торговля Российской Федерации.
Предмет исследования – разработка математической торговли РФ.
Цель исследования – выявление возможности применения модели Солоу для построения математической модели торговли РФ.
Методы исследования: дифференциальное исчисление, изоморфизм.
Торговля РФ это сложная социально-экономическая система. Системный подход к изучению сложной социально-экономической системы рассмотрен в [1,2,3,4].
Математическая модель описывает набор свойств (одно свойство) исследуемого объекта, так как все при попытке описать все свойства объекта исследования уменьшается адекватность модели. В нашем исследовании за основное свойство торговли РФ примем конечное потребление домашних хозяйств. Конечное потребление домашних хозяйств включает в себя:
1) расходы на товары (продовольственные и непродовольственные), кроме покупки жилищ и ценностей (дорогих предметов длительного пользования – антиквариат, драгоценности и т.д.; приобретаются, как правило, с целью инвестирования);
2) расходы на услуги.
Статистические данные торговли РФ позволяют оценить расходы домашних хозяйств на товары. Соответственно, конечное потребление домашних хозяйств будет учтено в части товаров, если математическая модель будет описывать только торговлю РФ. Конечное потребление, вероятно, должно находиться в некотором диапазоне: не меньше нормативного значения (например, нижняя граница – стоимость потребительской корзины за минусом стоимости услуг, верхняя граница – располагаемый доход домашнего хозяйства).
Соответственно, запишем ограничение для конечного потребления домашнего хозяйства:
FCn ≤ FC ≤ AI (1)
где FCn – нормативное конечное потребление на душу населения (final consumption normative);
FC – конечное потребление на душу населения (final consumption);
AI – среднедушевой денежный доход (average income)/
Торговля РФ выпускает, если так можно выразиться, единственный товар – продовольственные и непродовольственные товары (автор приносит свои извинения за тавтологию). Модель Солоу [5] также оперирует одним товаром. Возможно представление модели Солоу с дискретным временем и непрерывным временем. Также сама производственная функция Солоу может быть двухфакторной (2), двухфакторной CES (SMAC) (3) [6], многофакторной (4).
Y=(a1x1b1+a2x2b2)c (2)
где
Y – валовой внутренний продукт торговли РФ;
х1, х2 – независимые переменные;
а1, а2, b1, b2, c – константы;
а1, а2 строго больше ноля;
b1, b2, c одного знака.
Y=(a1x1b+a2x2b)c (3)
Y=(a1x1b1+a2x2b2+… +anxnbn)c (4)
Возникает шесть различных моделей и результаты их будут различаться. Помимо того, возможно упростить модель Солоу, встроив в неё (инкорпорировав) производственную функцию Кобба-Дугласа (5) [7].
(5)
где А – константа, отвечающая за технологии;
L – труд (среднегодовая численность занятых в торговле);
α – показатель степени при факторе «труд»;
К – капитал (основные фонды в торговле);
β – показатель степени при факторе «капитал».
Используя метод наименьших квадратов и данные статистики торговли РФ, можно оценить параметры L, α и β в (5).
Применяем ars magna Раймонда Луллия [8] и насчитываем восемь математических моделей торговли РФ (табл.1).
Таблица 1
Математические модели торговли РФ на основе модели Солоу
| № | Время | Производственная функция |
| 1 | Дискретное | Двухфакторная Солоу |
| 2 | Непрерывное | Двухфакторная Солоу |
| 3 | Дискретное | Двухфакторная Солоу CES (SMAC) |
| 4 | Непрерывное | Двухфакторная Солоу CES (SMAC) |
| 5 | Дискретное | Многофакторная Солоу |
| 6 | Непрерывное | Многофакторная Солоу |
| 7 | Дискретное | Кобба-Дугласа |
| 8 | Непрерывное | Кобба-Дугласа |
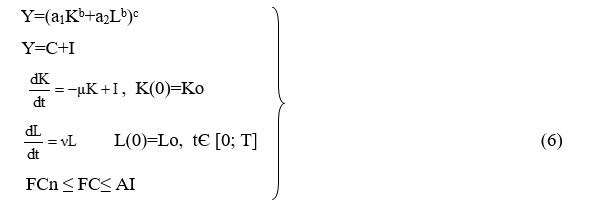
В качестве примера приведем модель №4 с непрерывным временем и двухфакторной производственной функцией Солоу (6)
где Y – валовой внутренний продукт торговли (все продовольственные и непродовольственные товары за год в денежном исчислении), производственная функция;
I – инвестиции в основной капитал торговли;
С – потребление, для торговли это все продовольственные и непродовольственные товары за год в денежном исчислении;
µ – коэффициент износа основных производственных фондов за год;
ν – темп прироста численности занятых в торговле;
Т – конечный год исследуемого периода времени.
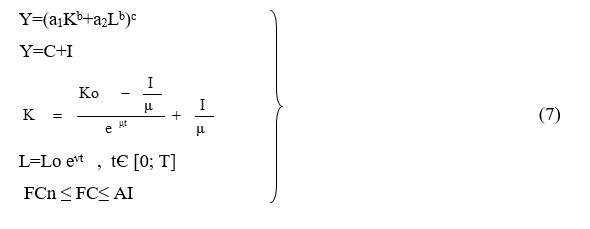
После интегрирования (6) выглядит следующим образом (7)
Результаты исследования.
- Предложены восемь математических моделей торговли РФ на основе модели Солоу.
- Математическая модель торговли РФ на основе модели Солоу дополнена ограничением по конечному потреблению.
- Математическая модель торговли РФ на основе двухфакторной производственной функции Солоу (CES) дана в развернутом виде.
- Предложено в модели торговли РФ на основе модели Солоу производственную функцию Солоу заменить на производственную функцию Кобба-Дугласа.
Библиографический список
1. Whitehead А.N. Process and reality. N.-Y.: Macmillan company, 1967. 546 p.2. L. Bertalanffy «Theoretische Biologie», Bd. I, Berlin, 1932. 122 p.
3. Ростова О.В., Ильин И.В. Методы информационного обеспечения инновационной деятельности // Наука и бизнес: пути развития. 2017. №2, с.30-35.
4. Ильин И.В. Зайченко И.М. Выбор стратегии развития предприятия на основе метода анализа иерархий // Наука и бизнес: пути развития. 2017. №1, с.29-36.
5. Solow R.M. Contribution to the theory of economic growth // Quarterly journal of economics. – 1956. – V.70 – P. 65-94.
6. Arrow K. J. Chenery H. B. Minhas B. S. Solow R. M. Capital-labor Substitution and Economic Efficiency // Rev. Econ. Stat. 1961. №43
7. Cobb W. Douglas P.H. A theory of production // The American Economic Review. Vol.18. №1.
8. Кульматов В. А. К истории распространения идей Луллия в России // Россия и гносис. М.: «Рудомино», 2000. — С.53-62.