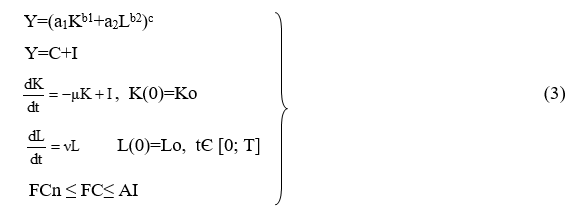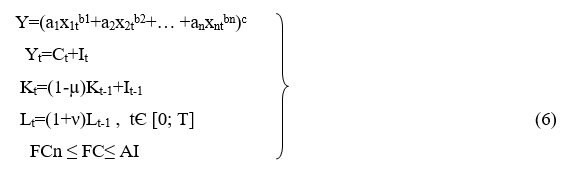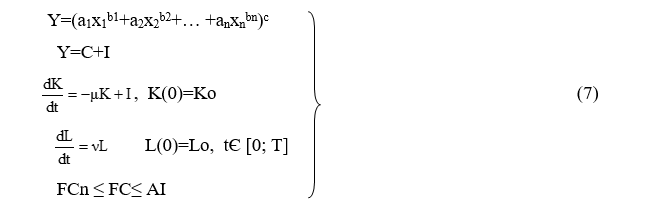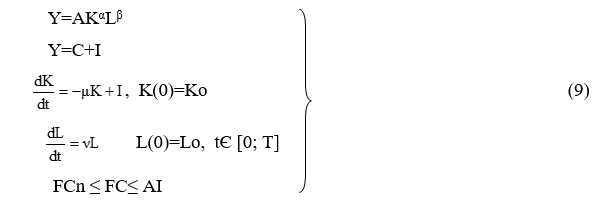Актуальность. В зависимости от выбранных свойств объекта исследования и от спецификации модели (предположение о виде связи между факторами и результатом) возникают различные математические модели объекта исследования. Последующая верификация позволяет выбрать оптимальный вариант модели.  Соответственно, наличие нескольких вариантов математических моделей повышает достоверность результата.

Объект исследования ­– математическая модель розничной торговли Российской Федерации.

Предмет исследования – описание математических моделей розничной торговли РФ.

Цель исследования – подробная детализация математических моделей розничной торговли РФ с тем, чтобы выбрать наиболее простой вариант для последующего решения.

Методы исследования: дифференциальное исчисление, изоморфизм.

Торговля РФ это сложная социально-экономическая система. Системный подход к изучению сложной социально-экономической системы рассмотрен в [1,2,3,4].

В предыдущем исследовании [5] уже было указано на существование восьми математических моделей розничной торговли РФ. В данной статье приведем детальное описание этих моделей. Ядро этих моделей – модель Солоу. Различается время: дискретное и непрерывное. Различается производственная функция (далее – ПФ): двухфакторная Солоу [6], двухфакторная Солоу (CES), многофакторная Солоу, ПФ Кобба-Дугласа [7]. Добавлено ограничение конечного потребления (в части продовольственных и непродовольственных товаров)

FCn ≤ FC ≤ AI                                                                                                                                                (1)

где FCn – нормативное конечное потребление на душу населения в части продовольственных и непродовольственных товаров (final consumption normative). Например, стоимость потребительской корзины за вычетом стоимости услуг;

FC – конечное потребление на душу населения (final consumption);

AI – среднедушевой денежный доход (average income).

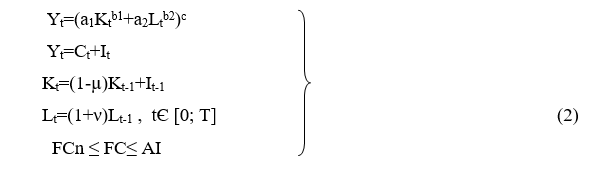
Модель №1. ПФ двухфакторная Солоу, время дискретное.

где а1, а2, b1, b2, c – константы;

а1, а2  строго больше ноля;

b1, b2, c – одного знака;

где Y – валовой внутренний продукт розничной торговли (все продовольственные и непродовольственные товары за год в денежном исчислении), производственная функция;

К – капитал (основные фонды в торговле);

L – труд (среднегодовая численность занятых в торговле);

С – потребление, для торговли это все продовольственные и непродовольственные товары за год в денежном исчислении;

I – инвестиции в основной капитал торговли;

µ – коэффициент износа основных производственных фондов за год;

ν – темп прироста численности занятых в торговле;

t=0 – базовый год;

Т – конечный год исследуемого периода времени.

Модель №2. ПФ двухфакторная Солоу, время непрерывное.

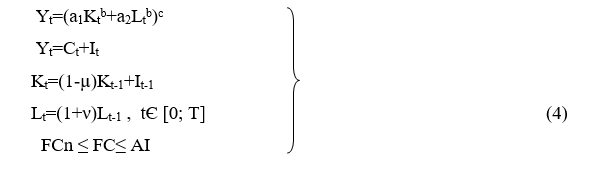
Модель №3. ПФ двухфакторная Солоу (CES), время дискретное.

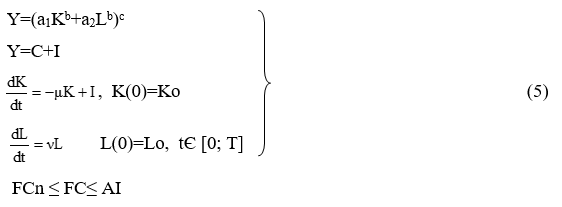
Модель №4. ПФ двухфакторная Солоу (CES), время непрерывное.

Модель №5. ПФ многофакторная Солоу, время дискретное.

где а1, …, аn, b1,…,  bn, c – константы;

а1,.., аn  строго больше ноля;

b1, .., bn, c – одного знака;

x_1t,.., x_nt – факторы ПФ.

Модель №6. ПФ многофакторная Солоу, время непрерывное.

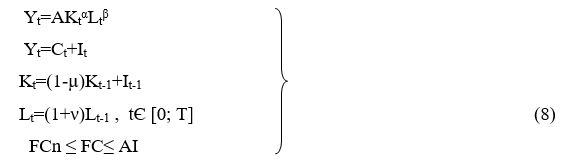
Модель №7. ПФ Кобба—Дугласа, время дискретное.

где А – константа, отвечающая за технологии;

α – показатель степени при факторе «капитал»;

β – показатель степени при факторе «труд».

Модель №8. ПФ Кобба-Дугласа, время непрерывное.

Результаты исследования.

1. Детально описаны восемь математических моделей торговли РФ на основе модели Солоу.
2. Ядро модели – модель Солоу. В ядро модели инкорпорировали ограничение по конечному потреблению.

Дальнейшее направление исследования – решить полученные математические модели, верифицировать их и выбрать оптимальную по критерию оптимального конечного потребления.