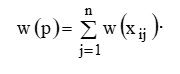Экономический объект – это лицо или группа лиц, занимающихся экономической деятельностью. Функционирование экономического объекта – это его переход из одного состояния в другое. Если условиться понимать состояния объекта как элемент некоторого множества состояний (множества вершин некоторого ориентированного графа состояний), а переход из состояния в состояние – считать ребрами этого ориентированного графа, то получаем модель функционирования объекта в виде построения определенного пути по ориентированному графу состояний. Применимость графов для моделирования показана в [1]. Анализируя графическую модель функционирования, легко увидеть, что она полностью адекватна другой дискретной математической модели, а именно, модели конечного автомата. Понятие конечного автомата применялось для моделирования механических и электронных устройств [2]. Формализация понятия экономического объекта и его состояний позволила использовать автомат для описания функционирования объекта экономики, когда входными сигналами являются ресурсы и внешние факторы.  Известно, что теоретической основой моделирования дискретных систем является теория экспериментов с конечными автоматами [3], базирующаяся на предположении, что входные последовательности одинаковой длины, подаваемые в процессе эксперимента на автомат, имеют и одинаковую «цену». Под ценой входной последовательности в классической теории понимается ее длина, то есть количество символов, входящих в эту последовательность. Если же цену интерпретировать как энергетические затраты на подачу входной последовательности, то предположение об одинаковых затратах на подачу равных по длине, но различных по составу последовательностей, оказывается, вообще говоря, неверным. Последнее объясняется тем, что с точки зрения энергетических затрат «цена» подачи, например, нулевого и единичного сигнала различна. Понятно, что при достаточно большой размерности входных последовательностей их «цены» при равной длине могут существенно отличаться. В связи с этим предпринята попытка построить фрагмент теории экспериментов с автоматами в условиях, когда каждому символу входного алфавита автомата поставлено в соответствие некоторое положительное число, далее называемое весом этого символа. Тогда весом входной последовательности будем называть сумму весов символов, входящих в эту последовательность. В отличие от классической теории экспериментов с автоматами, в условиях взвешенности символов входного алфавита иной смысл приобретает понятие минимальности эксперимента. Минимальным теперь будем называть эксперимент, которому соответствует подача на вход автомата минимальной по весу (но не по длине!) входной последовательности.

Под автоматом будем понимать пятерку объектов A = (S,X,Y,δ,λ), где S,X,Y – конечные множества состояний, входной и выходной алфавиты соответственно, δ, λ – функции переходов и выходов, задающие отображения

δ : S×X → S, λ : S×X → Y.

Через S₀ обозначим подмножество множества состояний S, которое назовем множеством допустимых начальных состояний автомата A. Под экспериментом, как и в [3], понимается процесс приложения входных последовательностей к автомату и вывода заключений, основанных на этих наблюдений. При этом предполагается, что в процессе эксперимента доступны только входные и выходные каналы автомата. Каждому входному символу x_i X поставим в соответствие некоторое положительное число w(x_i), называемое весом символа x_i. Весом входной последовательности p назовем число

При этом учитываются свойства полугруппы входных сигналов из [4].

Эксперимент, связанный с подачей синхронизирующей последовательности автомата, построен в [5].  Предлагаемая статья посвящена вопросу подачи установочной последовательности .

Входная последовательность p = x_i1, x_i2… x_in называется установочной для автомата A и множества допустимых начальных состояний S₀, если

С содержательной точки зрения это определение означает следующее: по наблюдаемой реакции на установочную последовательность автомата A, находящегося в известном начальном состоянии, всегда однозначно определяется его конечное состояние.

Задача построения последовательности с минимальным весом формулируется следующим образом. Задан конечный автомат А своей таблицей переходов и выходов и вес 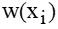 каждого символа  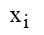 входного   алфавита   автомата  А.   Требуется   разработать   метод   построения установочной последовательности для заданного автомата, имеющей минимальный вес.

Синтез установочных последовательностей начнем с построения по таблице переходов-выходов заданного автомата графа, называемого графом установки (ГУА), который производится по аналогии с построением установочного дерева в [3].  Каждая его вершина отмечается А-группой σ-множеств и она используется в качестве имени соответствующей вершины.  Вершина называется простой, если соответствующая А-группа содержит только простые σ-множества. Вершина называется кратной, если соответствующая А-группа содержит кратное σ-множество. Вершина называется однородной, если соответствующая А-группа содержит только однородные σ-множества.  Способ трансформирования под воздействием входного символа x_i X А-группы, которой отмечена вершина S, в новую А-группу (вершину S^*) остается таким же, что определен в [3] при построении установочного дерева. Каждой вершине графа поставим в соответствие флажок, значение которого равно сумме весов входных символов последовательности, соответствующей пути по графу, ведущему из вершины S₀ в вершину S.

Процесс построения ГУА осуществляется рекурсивно, начиная с вершины S₀, затем последовательно строят вершины 1-го, 2-го  и следующих уровней, соединяемых между собой дугами, помеченными символами входного алфавита X.

Правила завершения установочного дерева в [3] таковы. Вершина S k-того уровня становится оконечной, если выполняется по крайней мере одно из условий:

1) она является однородной;

2) она является простой;

3) на уровнях, предшествующих k-тому, имеется вершина S^* такая, что S=S^* , но значение флажка  вершины S больше значения флажка вершины S^*;

4) на уровнях, предшествующих k-тому, имеется однородная или простая вершина S^* , значение флажка  которой меньше значения флажка вершины S.

Известно [6], что в графе типа дерева, если существует путь между двумя его вершинами, то он единственен. Из этого следует, что синтез минимальной по весу установочной последовательности сводится к следующей простой процедуре. Среди всех простых и однородных вершин ГУА отыскивается вершина S с минимальным значением флажка и в графе определяется единственный путь из S₀ в S, которому соответствует некоторая последовательность входных символов. Очевидно, что найденная последовательность и является установочной последовательностью.

В работе предложено обобщение понятия минимального эксперимента, предложен метод синтеза установочной последовательности, который по трудоемкости весьма незначительно отличается от известных классических методов.