Abstract: The author on the basis of function of Cobb-Douglas builds and investigates mathematical model of construction branch of the Russian Federation. The mathematical model of construction branch of the Russian Federation is expressed by production function. The author estimates the accuracy of the received mathematical model of construction branch of the Russian Federation.
Keywords: Mathematical model, system, production function, factor, approximation.
Актуальность исследования. Математическая модель сложной экономической системы позволяет с достаточной степенью точности отразить изучаемые свойства объекта исследования. Строительная отрасль является одной из ключевых в экономике народного хозяйства. В настоящее время, начиная с 2014г., объемы строительных работ в России сокращаются. Это не может не вызывать тревогу. Наличие математической модели строительной отрасли позволит указать пути выхода из сложившейся ситуации.
Рассмотрим в качестве математической модели строительной отрасли производственную функцию строительной отрасли, т.е. зависимость валового внутреннего продукта (далее – ВВП) строительной отрасли от основных факторов. Определив в качестве математической модели производственную функцию, мы тем самым сразу определили и основное исследуемое свойство изучаемой сложной экономической системы (строительной отрасли РФ) – ВВП. Адекватная математическая модель (далее – ММ) строительной отрасли позволит спрогнозировать поведение строительной отрасли России в зависимости от изменения факторов. Если в основе ММ строительной отрасли будут учтены значимые факторы, то она (ММ) может дать приемлемый прогноз будущего развития строительной отрасли.
Объект исследования – сложная экономическая система, а именно, строительная отрасль РФ.
Предмет исследования – математическая модель строительной отрасли РФ в виде производственной функции.
Цель исследования – построение и изучение математической модели строительной отрасли РФ на основе производственной функции.
Методы исследования – предварительная обработка данных (логарифмирование), регрессионный анализ.
Обратимся к математической модели строительной отрасли РФ в виде производственной функции (далее – ПФ). Производственную функцию в разное время изучали Кобб, Дуглас [1], Клейнер [2], Макаров [3], Ильин [4,5,6] и др.
Системный подход к сложным экономическим системам представлен в работах [7,8,9,10].
По мнению автора, для построения производственной функции строительной отрасли надо отобрать следующие факторы – рабочая сила L (занятые в строительстве), капитал K (основные фонды строительства). Соответственно, производственная функция строительной отрасли будет перекликаться с функцией Кобба-Дугласа.
Экономический смысл ПФ строительной отрасли – рост числа занятых и рост капитала в строительной отрасли должны приводить к росту ВВП. Так, по мнению автора, выглядит содержательная модель строительной отрасли РФ. В какой мере каждый фактор отвечает за рост ВВП строительной отрасли, должны показать результаты исследования. Для этого содержательную модель опишем языком математики, за основу взяв ПФ Кобба-Дугласа.
(1)
где C – константа, связанная с уровнем технологий, применяемых в строительстве;
L– занятые в строительстве, тыс. чел.);
α – показатель степени при факторе «занятые в строительстве»;
K – основные фонды строительства, млрд. руб.;
β – показатель степени при факторе «основные фонды строительства».
Y – ВВП строительной отрасли, млрд. руб. в год.
После логарифмирования Y, мы получим выражение приемлемое для исследования статистических данных
lnY=lnC + αlnL+ βlnK (2)
Рассмотрим статистику строительной отрасли РФ (табл.1). [11]
Таблица 1
Данные о строительной отрасли РФ за 2005-2015г.г.*
| Год | ВВП строительства, млрд. руб. | Основные фонды в строительстве, млрд. руб. | Численность занятых в строительстве, тыс. чел. |
| 2005 | 989,9 | 604,922 | 4578,712 |
| 2006 | 1 202,0 | 711,286 | 4495,967 |
| 2007 | 1 633,9 | 992,921 | 4953,921 |
| 2008 | 2 225,3 | 1220,893 | 5396,232 |
| 2009 | 2 101,5 | 1391,117 | 4928,142 |
| 2010 | 2 587,8 | 1499,94 | 5035,226 |
| 2011 | 3 962,9 | 1553,038 | 5101,676 |
| 2012 | 4 524,3 | 1581,874 | 5294,360 |
| 2013 | 4 474,8 | 1676,906 | 5425,750 |
| 2014 | 4 681,5 | 1774,655 | 5436,964 |
| 2015 | 4 780,3 | 2049,423 | 5496,595 |
*- составлено автором по данным Росстата
Логарифмирование данных приведет к табл.2.
Таблица 2
Промежуточные данные для анализа ПФ строительной отрасли РФ
| Год | lnY | lnК | lnL |
| 2005 | 6,898 | 6,405 | 8,429 |
| 2006 | 7,092 | 6,567 | 8,411 |
| 2007 | 7,399 | 6,901 | 8,508 |
| 2008 | 7,708 | 7,107 | 8,593 |
| 2009 | 7,650 | 7,238 | 8,503 |
| 2010 | 7,859 | 7,313 | 8,524 |
| 2011 | 8,285 | 7,348 | 8,537 |
| 2012 | 8,417 | 7,366 | 8,574 |
| 2013 | 8,406 | 7,425 | 8,599 |
| 2014 | 8,451 | 7,481 | 8,601 |
| 2015 | 8,472 | 7,625 | 8,612 |
Регрессионная зависимость выглядит:
lnY=-14,794 + 1,693lnL + 1,147lnK (3)
Y=e -14,794 x L 1,693 x K 1,157 (4)
Коэффициент множественной корреляции равен 0,9545, это указывает на сильную связь всех факторов с результатом.
Статистическая значимость всего уравнения подтверждается фактическим значением критерия Фишера 40,9. Зависимость нелинейная, что подтверждает сложность экономической системы.
Коэффициент эластичности по труду равен 1,693. Коэффициент эластичности по капиталу равен 1,157. Следовательно, рост числа занятых оказывает большее влияние на рост ВВП строительной отрасли, нежели рост капитала. Соответственно, по данным полученной ММ основной путь выведения строительной отрасли из нынешнего плачевного состояния – увеличение числа занятых в строительстве. Коэффициент технологии в данной ММ очень мал и с трудом может быть интерпретирован. Предполагается, что предварительная обработка данных должна включить в себя нормирование данных для исключения фактора размерности. Тогда коэффициент С будет вполне экономически объяснимым.
Проведем сравнение фактических и расчетных данных, полученных по зависимости (4) .
Таблица 3
Сравнение фактических и расчетных значений ВВП строительной отрасли РФ за 2005-2015г.г.
| Год | ВВПфакт, млрд. руб. | ВВПрасчет, млрд. руб. |
| 2005 | 989,9 | 923,2 |
| 2006 | 1 202,0 | 1 078,0 |
| 2007 | 1 633,9 | 1 862,8 |
| 2008 | 2 225,3 | 2 729,2 |
| 2009 | 2 101,5 | 2 718,6 |
| 2010 | 2 587,8 | 3 073,9 |
| 2011 | 3 962,9 | 3 270,9 |
| 2012 | 4 524,3 | 3 557,1 |
| 2013 | 4 474,8 | 3 964,6 |
| 2014 | 4 681,5 | 4 245,7 |
| 2015 | 4 780,3 | 5 101,5 |
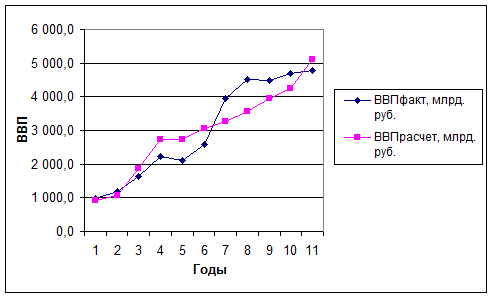
Графически это сравнение отражено на рис.1
Рисунок 1. Сравнение фактических и расчетных значений ВВП строительной отрасли
Есть сходимость между фактическими и расчетными значениями ВВП строительной отрасли.
Результаты исследования.
1) Построена математическая модель строительной отрасли РФ в виде производственной функции.
2) Указаны наиболее существенные факторы, влияющие на ВВП строительной отрасли – число занятых в строительстве; основные фонды строительства. Найдены коэффициенты эластичности при факторе «число занятых в строительстве» и при факторе «основные фонды строительства».
3) По данной математической модели рост занятых в строительстве оказывает большее влияние на ВВП строительства, чем увеличение основных фондов.
Библиографический список
1. Cobb W. Douglas P.H. A theory of production // The American Economic Review. Vol.18. №1.2. Клейнер Г.Б. Производственные функции: теории, методы, применение. М.: Финансы и статистика, 1986г.
3. Макаров В.Л. Вычислимая модель российской экономики (RUSEC) /Препринт № wp/99/069. М.: ЦЭМИ РАН, 1999г.
4. Ростова О.В., Ильин И.В. Методы информационного обеспечения инновационной деятельности // Наука и бизнес: пути развития. 2017. №2, с.30-35.
5. Левина А.И., Ильин И.В., Эседулаев Р.А. Повышение эффективности проектов внедрения информационных систем класса BPMS с использованием типовых проектных решений // Наука и бизнес: пути развития. 2017. №4, с.9-14.
6. Ильяшенко О.Ю., Ильин И.В., Болобонов Д.Д.Роль BI-систем в совершенствовании процессов обработки и анализа бизнес-информации // Наука и бизнес: пути развития. 2017. №6, с.124-131.
7. Никоноров В.М. Устойчивость системы: экономический аспект // Современная научная мысль. 2017. №3. С. 154-158.
8. Никоноров В.М. Оценка производственной функции розничной торговли Российской Федерации // Вопросы современной науки и практики. Университет им. В. И. Вернадского, 2017-№3 (65), с.103-109.
9. Никоноров В.М. Уточненная оценка производственной функции розничной торговли Российской Федерации // Общество: политика, экономика, право, 2017-№9, с.32-36.
10. Никоноров В.М., Шотт Р. В. Теоретические основы экономики и управления в сфере услуг: Учебное пособие – СПб.: Изд-во СПбПУ, 2017. – 100 с.
11. Суринов А.Е. Российский статистический ежегодник 2016: Стат.сб./Росстат. - Р76 М., 2016 – 725 с.