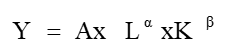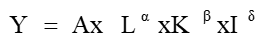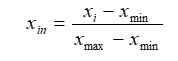Abstract: The author has considered one-sector economy. Production function I have assumed multiplicative function as a basis. Unlike function of Cobb-Douglas has added an additional expensive factor - "information". On reliable statistical material I have found dependence between GDP of the Russian Federation and expensive factors: work, capital, information. I have checked approximation by the found function calculated and the GDP actual values of the Russian Federation.
Keywords: Production function, work, capital, information, linearization.
Актуальность. Производственная функция (далее – ПФ) экономики РФ отражает зависимость валового внутреннего продукта (далее – ВВП) от затратных факторов. Соответственно, вид ПФ позволит определить является ли эта ПФ неоклассической, с возрастающей отдачей или убывающей, ресурсосберегающей или трудосберегающей. Эта информация укажет пути дальнейшего роста ВВП РФ.
Объект исследования – экономика Российской Федерации.
Предмет исследования – разработка производственной функции экономики РФ.
Цель исследования – выявление взаимосвязи между ВВП РФ и факторами производства.
Методы исследования: линеаризация данных, метод наименьших квадратов (поиск регрессионной зависимости).
Производственную функцию в разное время изучали Кобб, Дуглас [1], Клейнер [2], Макаров [3], Ильин [4] и др. За основу возьмем производственную функцию Кобба-Дугласа. Это мультипликативная функция
где А – константа, отвечающая за технологии;
L – фактор «труд» (среднегодовая численность занятых);
α – показатель степени при факторе «труд»;
К – фактор «капитал» (основные фонды в экономике);
β – показатель степени при факторе «капитал»;
Y – ВВП РФ.
Рабочая гипотеза исследования: автор предполагает, что начиная с 80-ых годов XX века (появление персональных компьютеров) следует учитывать также фактор «информация». Соответственно, в данном исследовании мы проанализируем статистические данные за период 2005-2016г.г. на предмет установления связи (отсутствия связи) между ВВП РФ и факторами производства – труд, капитал, информация. Функция (1) приобретает вид
где I – фактор «информация» (затраты на информационные и коммуникационные технологии);
δ – показатель степени при факторе «информация».
Рассмотрим данные за 2005-2016г.г. (табл.1).
Таблица 1
Показатели экономики РФ [5]*
| № | Год | Y, млрд. руб. | L, тыс. чел. | K, млрд. руб. | I, млрд. руб. |
| 1 | 2005 | 21 610 | 66 792 | 41 494 | 168 |
| 2 | 2006 | 26 917 | 67 174 | 47 489 | 252 |
| 3 | 2007 | 33 248 | 68 019 | 60 391 | 299 |
| 4 | 2008 | 41 277 | 68 474 | 74 441 | 373 |
| 5 | 2009 | 38 786 | 67 463 | 82 303 | 421 |
| 6 | 2010 | 46 309 | 67 493 | 93 186 | 516 |
| 7 | 2011 | 59 698 | 67 644 | 108 001 | 603 |
| 8 | 2012 | 66 927 | 67 968 | 121 269 | 842 |
| 9 | 2013 | 71 017 | 67 901 | 133 522 | 1 246 |
| 10 | 2014 | 79 200 | 67 813 | 147 430 | 1 175 |
| 11 | 2015 | 83 233 | 72 425 | 160 725 | 1 184 |
| 12 | 2016 | 86 044 | 72 065 | 183 404 | 1 249 |
*-составлено автором по данным gks.ru
Нормируем данные методом минимакса, чтобы устранить эффект размерности
где Xin- нормированное значение Xi;
Xmax – максимальное значение фактора;
Xmin – минимальное значение фактора.
Нормированные данные представлены в табл.2
Таблица 2
Нормированные показатели экономики РФ за 2005-2016г.г.
| № | Год | Yn | Ln | Kn | In |
| 1 | 2005 | — | — | — | — |
| 2 | 2006 | 0,082 | 0,072 | 0,042 | 0,078 |
| 3 | 2007 | 0,181 | 0,233 | 0,133 | 0,121 |
| 4 | 2008 | 0,305 | 0,319 | 0,232 | 0,190 |
| 5 | 2009 | 0,267 | 0,127 | 0,288 | 0,234 |
| 6 | 2010 | 0,383 | 0,133 | 0,364 | 0,322 |
| 7 | 2011 | 0,591 | 0,162 | 0,469 | 0,402 |
| 8 | 2012 | 0,703 | 0,223 | 0,562 | 0,623 |
| 9 | 2013 | 0,767 | 0,210 | 0,648 | 0,997 |
| 10 | 2014 | 0,894 | 0,194 | 0,747 | 0,932 |
| 11 | 2015 | 0,956 | 1,068 | 0,840 | 0,940 |
| 12 | 2016 | 1,000 | 1,000 | 1,000 | 1,000 |
Линеаризуем (прологарифмируем) нормированные данные (табл.3). При этом уровень 2005г. выпадет из рассмотрения как ln(0).
Таблица 3
Линеаризованные показатели экономики РФ
| № | Год | lnYn | lnLn | lnKn | lnIn |
| 2 | 2006 | — 2,497 | — 2,625 | — 3,164 | — 2,555 |
| 3 | 2007 | — 1,711 | — 1,458 | — 2,016 | — 2,110 |
| 4 | 2008 | — 1,187 | — 1,143 | — 1,460 | — 1,663 |
| 5 | 2009 | — 1,322 | — 2,062 | — 1,246 | — 1,452 |
| 6 | 2010 | — 0,959 | — 2,018 | — 1,010 | — 1,133 |
| 7 | 2011 | — 0,526 | — 1,823 | — 0,758 | — 0,910 |
| 8 | 2012 | — 0,352 | — 1,500 | — 0,576 | — 0,472 |
| 9 | 2013 | — 0,266 | — 1,559 | — 0,433 | — 0,003 |
| 10 | 2014 | — 0,112 | — 1,642 | — 0,292 | — 0,071 |
| 11 | 2015 | — 0,045 | 0,066 | — 0,174 | — 0,062 |
| 12 | 2016 | 0,000 | 0,000 | 0,000 | 0,000 |
Применим регрессионный анализ (метод наименьших квадратов).
Регрессионная зависимость выглядит:
lnYn=0,07+ 0,036lnLn+0,513lnKn + 0,333lnIn (4)
Yn=1,07 x Ln 0,036 x Kn 0,513 x In 0,333 (5)
Очевидно, что значения ПФ расположены в положительной части пространства х, функция выпукла вверх и монотонно увеличивается с ростом аргументов. Если задать цену каждого фактора и бюджетное ограничение, то можно решить задачу на экстремум ПФ.
Производственная функция экономики РФ задает экономико-математическую модель (далее – ЭММ) экономики страны. Оценим качество полученной ЭММ.
Проверка зависимости приводит к табл.4
Таблица 4
ВВП РФ (фактический и расчетный)
| № | Год | Ynфакт | Ln | Kn | In | Ynрасчет |
| 2 | 2006 | 0,082 | 0,072 | 0,042 | 0,078 | 0,082 |
| 3 | 2007 | 0,181 | 0,233 | 0,133 | 0,121 | 0,179 |
| 4 | 2008 | 0,305 | 0,319 | 0,232 | 0,190 | 0,280 |
| 5 | 2009 | 0,267 | 0,127 | 0,288 | 0,234 | 0,324 |
| 6 | 2010 | 0,383 | 0,133 | 0,364 | 0,322 | 0,408 |
| 7 | 2011 | 0,591 | 0,162 | 0,469 | 0,402 | 0,503 |
| 8 | 2012 | 0,703 | 0,223 | 0,562 | 0,623 | 0,646 |
| 9 | 2013 | 0,767 | 0,210 | 0,648 | 0,997 | 0,812 |
| 10 | 2014 | 0,894 | 0,194 | 0,747 | 0,932 | 0,850 |
| 11 | 2015 | 0,956 | 1,068 | 0,840 | 0,940 | 0,963 |
| 12 | 2016 | 1,000 | 1,000 | 1,000 | 1,000 | 1,073 |
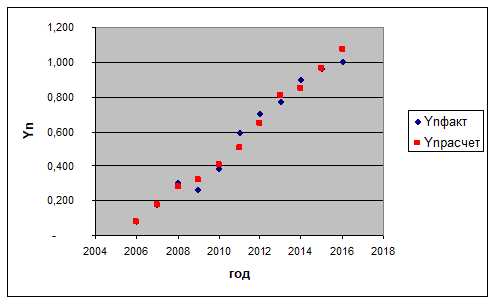
На графике эта зависимость выглядит (рис.1).
Рисунок 1. Расчетные и фактические значения ВВП РФ за 2005-2016г.г.
Сходимость присутствует.
Очевидно, что значения ПФ расположены в положительной части пространства х, функция выпукла вверх и монотонно увеличивается с ростом аргументов. Найденная ПФ неоклассическая (это можно легко проверить). Полученная ПФ с убывающей отдачей от факторов производства. Соответственно, данная ПФ статична, так как коэффициенты эластичности не меняются во времени.
Результаты исследования.
- Рассчитана производственная функция экономики РФ. Производственная функция определяет экономико-математическую модель экономики страны.
- Определены коэффициенты эластичности при соответствующих затратных факторах.
- Функция Кобба-Дугласа дополнена затратным фактором «информация». Полученная ПФ показывает значимость этого фактора.
Библиографический список
1. Cobb W. Douglas P.H. A theory of production // The American Economic Review. Vol.18. №1.2. Клейнер Г.Б. Производственные функции: теории, методы, применение. М.: Финансы и статистика, 1986г.
3. Макаров В.Л. Вычислимая модель российской экономики (RUSEC) /Препринт № wp/99/069. М.: ЦЭМИ РАН, 1999г.
4. Ильин И.В., Широкова С.В., Эссер М. Управление проектами. Основы теории, методы, управление проектами в области информационных технологий / Санкт-Петербург, 2015.
5. Суринов А.Е. Российский статистический ежегодник 2016: Стат.сб./Росстат. - Р76 М., 2016 – 725 с.