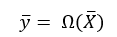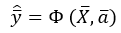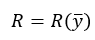The modern chemical industry faces many challenges, the most important of which are improving process efficiency and reducing costs. Optimisation of chemical processes plays a key role in achieving these goals, as it allows to find the best balance between various factors affecting performance and economic benefits. One of the most promising approaches is the use of mathematical models that take into account a large number of variables to find the optimal solution. The application of such models provides a significant increase in production efficiency, cost reduction and increase in the output of the final product. The present work is devoted to the analysis of the application of mathematical methods in the optimisation of chemical processes and the evaluation of their economic benefits. In particular, linear and nonlinear programming methods, as well as dynamic programming, which are widely used in the chemical industry, are considered. It is important to note that optimisation of processes using mathematical models allows not only to improve the technical characteristics of production, but also to ensure its economic sustainability. Examples from real production practice confirm the high significance of this approach for the chemical industry.

Processes associated with chemical technology are very complex. These are, first of all, chemical transformations in apparatuses of various designs due to the peculiarities of chemical reactions, multicomponent and multistage nature of many of them, and the need for catalysis. Mass-exchange processes, in particular rectification processes of multicomponent mixtures, widely used in preparation of raw materials for chemical transformations and separation of reaction products or separation of unreacted components of raw materials from the product stream, are no less complicated. At present, combined reaction-rectification processes are widely used as more energy and resource saving and ergonomic. Heat exchange processes are an integral part of any chemical production. Their efficiency depends on the design of apparatuses, properties of heat carriers and a number of technological parameters.

Chemical processes can be classified according to various criteria, depending on their nature and characteristics. The main groups of chemical processes include:

— Hydrodynamic processes: related to the movement of liquids and gases.

— Thermal processes: divided into equilibrium and non-equilibrium, as well as reversible and irreversible. These processes affect changes in temperature and state of matter.

— Diffusion processes: concern the movement of particles in space and their mixing.

— Chemical processes: involve reactions between substances leading to the formation of new substances.

— Mechanical processes: involve changes in the shape or position of substances without changing their chemical composition.

The ultimate goal of chemical process modelling (CPM) is to better implement or optimise a chemical process. Optimisation of chemical processes is aimed at achieving the best technical and economic performance. The key objectives of optimisation are:

— Increasing product yield: maximising the quantity of the target product with minimum resource input.

— Cost reduction: reducing raw material, energy and labour costs.

— Improving product quality: ensuring that products are consistent and meet specified standards.

— Environmental compliance: minimising the negative impact on the environment.

— Improving process safety: reducing the risks of accidents and incidents in production.

Optimisation methods may include analytical approaches, mathematical programming and statistical methods. It is important to take into account the physico-chemical characteristics of the process in order to effectively formulate optimisation problems and find the best solutions.

Modern achievements in the field of computer modelling of chemical processes make it possible to solve the problems of design and control of chemical plants more rigorously and with greater accuracy. The methodology of system analysis is widely used, with the application of which the problems of analysis, optimisation and synthesis of new and reconstructed technologies are successfully solved.

Computer modelling of chemical-technological processes involves solving the following main tasks:

— construction of a mathematical model of the process and its implementation on the computer;

— identification (identification) of the developed mathematical model with the modelled process in order to ensure its adequacy, i.e. qualitative and quantitative correspondence of the model to the real process;

 — optimisation of the process using its mathematical model, i.e. determination of optimal mode and design parameters of the processes, which provide the highest or lowest value of the selected optimality criterion characterising the efficiency of the real process.

It should be noted that computer modelling of CTP does not do without building a mathematical model, which plays a key role in the analysis and design of chemical processes. Building a mathematical model allows to predict the behaviour of the system under various conditions, which is extremely important for the development of efficient and safe production processes. The main methods include differential reaction equations, fluid flow modelling, thermodynamic calculations and others. Mathematical modelling is also used to develop new materials, including catalysts and polymers. The models help predict the properties of materials before they are created in material form, which reduces the time and cost of experimental research.

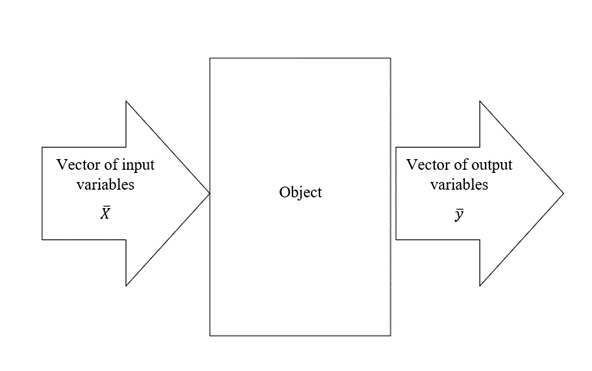
To solve computer modelling problems, the system approach is used, according to which the chemical-technological process (CTP) is considered as a functional system characterised by the following main sets of variables:

1)  is a vector of input variables that affect the state of the process and, in general, determine its state;

2)  is a vector of output variables that characterise the state of the process and depend on the input variables .

Figure 1. Schematic representation of CTP as a functional system

The system approach makes it possible to carry out mathematical formalisation of the problem when building mathematical models of both processes in individual devices and in the aggregate. Any system consists of interconnected and interacting parts and, in a certain sense, represents a closed whole. An object that is a set of interconnected apparatuses (chemical production), in particular for the production of some target product, is called a chemical technological system (CTS).

To represent the dependence of output variables  on input variables , a physical-chemical operator (for FHS) or a chemical-technological operator (for CTS) is used Ω

                          (1.1)

In expression (1.1) the operator Ω maps the space of input variables  into the space of values of output variables . The mapping (1.1) reflects all actually occurring processes and is a representation of objective reality, for which it is necessary to construct an approximate mathematical model of the process.

The most important stage of constructing an adequate mathematical model of chemical processes is the analysis of the structure of the chemical-technological or physical-chemical operators Ω (1.1). In this case the decomposition of a complex system into simpler subsystems is carried out in accordance with the following principles:

1. a) determining the hierarchical structure of the system, i.e., identifying its hierarchical stages and the interrelationships between them on the basis of fundamental knowledge, experimental data and experience of specialists;
2. b) implementation of the principle of hierarchical subordination when formalising knowledge about the studied elements of the system and making reasonable assumptions, which is expressed in taking into account the most important (priority) processes occurring at the lower levels of the system hierarchy and influencing the processes at the upper levels of the hierarchy;
3. c) a comprehensive study of individual processes, taking into account the influence of variables not only at the considered level of the system hierarchy, but also at lower levels and at higher levels of the system hierarchy.

Since the structure of the chemical-technological or physical-chemical operator is thoroughly unknown, the functional operator Φ (1.2), which is an approximation of the true operator Ω (1.1), is used instead.

The transformation of input variables  into estimates of output variables   can be mapped using the functional operator Φ:

                         (1.2)

where Φ is a functional operator that maps the space of input variables  into the space of estimates of output variables ;  are the coefficients of equations describing physicochemical processes. Relationship (1.2) is a system of equations of mathematical description (MD) of chemical-technological process (CTP) with initial and boundary conditions.

The ultimate goal of chemical process modelling (CPM) is its better implementation or its optimization. Optimisation is a purposeful activity, which consists in obtaining the best results (values of object parameters) under appropriate conditions. Optimisation consists in finding the extremum of the function under consideration or optimal conditions for carrying out a technological process. To assess the optimum, it is necessary first of all to choose an optimisation criterion.

An optimisation (optimality) criterion is a quantitative assessment of the optimised quality of an object. Successful solution of the optimisation problem is determined, first of all, by the correct choice of the optimality criterion or target function, which should fully characterise the efficiency of the technological process, taking into account the requirements that are the highest priority in solving a particular problem. This is due to the fact that the result of solving an optimisation problem may depend on the type of mathematical expression of the optimality criterion (target function). Therefore, in practice it is often necessary to solve multi-criteria (multiobjective) optimisation problems using weight coefficients of several criteria (target functions) combined into one optimality criterion.

In this case, the optimality criterion (target function) R must necessarily be characterised by some numerical indicator, i.e. be quantitative, and depend on the process variables, in particular, on the output (dependent) production variables ( ).

The type of functional dependence of the optimality criterion (target function) on output (dependent) variables is as follows:

                                (1.3)

depends on the type of selected criterion (technological, economic, technical-economic, thermodynamic, etc.) and, as a rule, is set by specialists.

Application of mathematical models for optimisation of chemical processes brings significant economic benefits expressed in reduction of production costs, increase of product yield and improvement of its quality. Let us consider the main aspects of economic efficiency of using mathematical methods.

One of the main tasks of the chemical industry is to minimise raw material and energy costs. Mathematical models make it possible to accurately calculate the required amount of reagents and optimise process parameters such as temperature, pressure and reaction time. This leads to a reduction in excess resource consumption and lower operating costs. For example, in the case of the synthesis of a complex organic compound, optimisation can lead to a reduction in the consumption of expensive solvent or catalyst, significantly reducing overall production costs.

Using mathematical models, it is possible to accurately predict the behaviour of the system and select the conditions under which the product yield is maximised. This is achieved by taking into account many factors such as reaction kinetics, thermodynamic parameters and the mutual influence of the mixture components. For example, in the polymerisation process, proper control of temperature and monomer concentration can significantly increase polymer yields, leading to increased profitability.

Product quality is determined by compliance with standards and specifications. Mathematical models can control critical process parameters such as purity, molecular weight and particle distribution to ensure that products meet the required specifications. This is particularly important in the pharmaceutical and food industries, where deviations from the standard can have serious consequences. Thus, the application of mathematical methods improves the stability and reliability of the production process, minimising rejects and increasing customer satisfaction.

Using «Наука» as an example, let’s look at how chemical process modelling can optimise production and reduce costs.

The scope of application of modelling is vast. These can be enterprises of oil refining, petrochemical, gas, chemical and power industries. «Наука» has developed an enlarged model of an oil refinery, which takes into account the influence of external and internal factors on the production process: technological and economic constraints, feedstock supply and shipment plans. As a result of the work performed, the company started saving 50 million rubles per month on energy resources alone, eliminated expensive additives, optimised feedstock supplies when considering different volumes of oil refining, and set up automated control and reporting of all processes. It also ensured the formation of a commodity basket with a minimum quality margin in accordance with national standards requirements. This allowed to reduce the total cost of goods produced and thereby increase the refinery’s profit.

The use of mathematical models at large industrial enterprises gives business a number of advantages.

1. The accuracy of production planning increases. It becomes possible to calculate the optimal parameters of the mode of technological objects at varying volumes of processing and quality of raw materials.
2. Optimisation of technological processes is provided. Mathematical models allow to adequately describe all types of substance and energy transformations occurring at the technological object. With their help it is possible to analyse the possibility and assess the feasibility of expanding the bottlenecks of chemical-technological systems.
3. Time and financial costs for optimisation are reduced. Thanks to mathematical models there is no need to carry out expensive and labour-intensive tests at operating industrial facilities. There is also an opportunity to obtain technical and economic assessments of the effectiveness of structural or parametric transformations of chemical process plants.
4. The efficiency of design of new and reconstruction of operating facilities increases. Mathematical models allow to carry out structural and parametric optimisation of design objects (units, installations, plants), to receive reliable data on performance of design works for introduction of new objects, reconstruction or technical re-equipment of existing ones. In this case, the accuracy of calculations of parameters and technological norms increases, capital and operating costs of the enterprise are reduced.